35993 skryptE

IMPLEMENTACJA ALGORYTMÓW CYFROWEJ FILTRACJI ORTOGONALNEJ

Rys. 7.3.

% deklaracja rzędu parametryzacji Schura

N«40j

fxl) « genlT, 0.05.0.10,0.15.0.20) ; pauaej

Ix| - Btncj(xl,N);

[xc| *» cntr <x) ;

[xsl « 3tnd(xc);

(a.r.rho) ■ innov(xb,N); inp=randn(T,1);

(inpc) » cntr(inp);

(inps) » atnd(inpc);

(ee.rr.yl *> model (rho, inps) ;

(cx,ccx,nccx] ■ koral(x8,K);

(cy.ccy.nccy) » korel(y.K);

(Wx,wx) ■ wqmx(x9);

(Wy.wyl » wgmx(y);

subplot (2.3.1) ; płot(xa/max(xa)): orid; titleCa)’); subplot (2.3.2) ; plot (nccx. ccx/max (ccx) ) ; grid; titleCb) ')» subplot(2,3,3); plot<wx/pi,wx/max(Wx))_; grid; titleCc)); subplot (2,3.4) ; plot (y/max(y) ) ; grid; title<’d)’); subplot (2.3. S) ; plot (nccy, ccy/max (ccy) ) ; grid; titLeCo)’); subplot(2.3.6) ; plot (wy/pi . Wy/max (Wy) > ; grid; titleCf)'):

Wyniki symulacji przedstawia rys. 7.3.

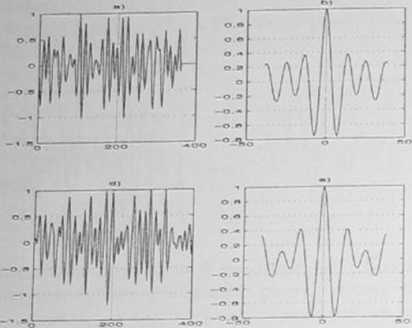
Wyniki symulacji w przykładzie 7.6: a) sygnał wejściowy filtru innowacyjnego. bi kowariancja sygnału wejściowego filtru innowacyjnego, c) wgm sygnału wejściowego filtru innowacyjnego, d) sygnał wyjściowy filtru modelującego, e) kowariancja sygnału wyjściowego filtru modelują cego. 0 wgm sygnału wyjściowego filtru modelującego

PRZYKi VD7.7 \daptacyjna filtracja innov    biegów czasowych

Przykład (m-plik P7 .m) ilustruje działanie filtru innowacyjnego o parametrach zmiennych w czasie, z adaptacyjnym uaktualnianiem w czasie wartości współ

180

rn-TRACJ, OBTOnn.m ... ,

" ^p,"'^kd' ^{6 3 3}-”-p'»" 7.‘ K

;    filtr.ci. innow.oyin,    „_a!>owy<:h

elear;    ......................

T^e20Q •

_Ka5. *    ' deklaracja długości syqnalu

NOÓ.    ^dlT’^{Cl fUnl}"^{jl !}'⁰“'"-ian_cn

1anbda=1;    ,, dekt! . " P»r»m.try«ej1 Schura

W - h«n₍T.o.o₅.o.,o,n o 251* ^WBpolc*’™^lk» »P««ln.ni,

(xcj - cntr (x) j

le.r.rho) = leemorf(xc,N,lambda)•

(xsj = 9tnd(xc);

(cx.ccx,nccx) = korel(xg.K); lce.ccc.ncce) - korel(eN),K>;

(Wx,wx) = wgmx(x9);

(Wrho4, wrhol ³ wqmx (rho (: , 4) ) j

subplot (2.2. l»; plot(xs) ; grid; titleCa)'):

3ub_Pl°t(2,2.2>; plot(wx/pi,Wx/max(Wxl); grid; title('c)')• subplot 2.2.3); plot < rho ( : . 4 ) ) _{: qrid:} tUleCb)’),    '

subplot (2.2,4) plot (wrho/pi , Wrho4/max (Wrhol) ) _; grid; titleCd)');

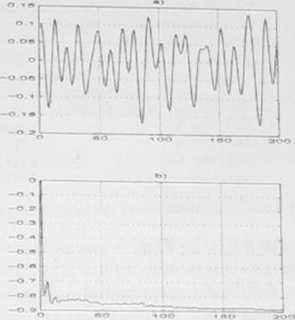
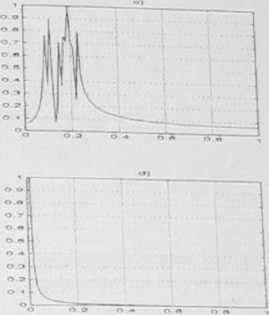
Wyn,k, symulacji pr7.eds.awia rys 7.4 Jak widać. wspńlczynniki Schura sa funkcjami wolnozmiennymi. a w konsekwencji zajmowane przez nie pasmo częstotliwości jest wielokrotnie węższe od pasma sygnału parametryzowanego.

Rys. 7 4

Wyniki symulacji w przykładzie 7.7 a) sygnał wejściowy filtru innowacyjnego, b) współczynnik Schura (n = 3). c) wgm sygnału wejściowego filtru innowacyjnego, d) widmo współczynnika Schura (n = 3)

181

inni

Implementacja algorytmów cyfrowej filtracji ortogonalne

Symulacje algorytmów cyfrowej filtracji ortogonalnej

Rys. 7.5

Potwierdza to wnioski przedstawione w punkcie 6.8. dotyczące metody LPC transmisji sygnałów.

PRZYKł M> 7.8 Adaptacyjne modelowanie stochastyczne szeregów czaso-wych

Przykład ilustruje działanie ortogonalnego filtru modelującego o parametrach zmiennych w czasie, realizującego adaptacyjne modelowanie szeregów cza sowych. Wejściowy szereg czasowy jest parametryzowany za pomocą adaptacyjnego filtru innowacyjnego (funkcja leemorf .m). Wyznaczone zmienne w czasie współczynniki Schura (rho) są wykorzystywane w filtrze modelują cym o parametrach zmiennych w czasie (funkcja mor f lee. m, implementująca algorytm opisany w punkcie 6.4). Sygnałem wejściowym filtru modelującego jest szerokopasmowy standaryzowany szereg czasowy inps tand Postać źródłowa m-pliku P8 .m jest następująca:

% P8.m Adaptacyjne modelowanie stochaetyczne sygnałów

% ...................................................

elear;

T°250;    ł.    deklaracja    długości sygnału

K=25;    %    deklaracja    długości funkcji kowariancji

N=20;    %    deklaracjo    rzędu parametryzacji Schura

lambda=l;    %    deklaracja    współczynnika zapominania

(x! - gentT.0.05,0.10,0.20,0.25);

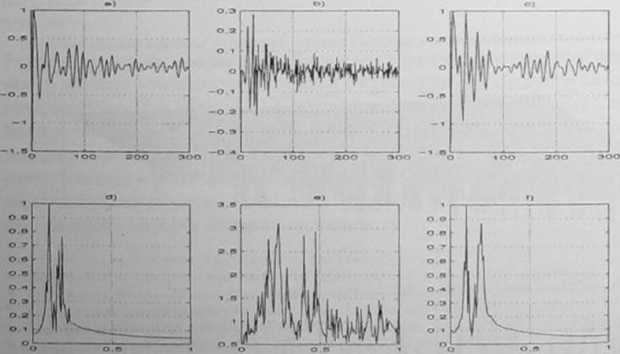
Wyniki symulacji w przykładzie 7.8: a) sygnał wejściowy filtru innowacyjnego; b) sygnał wejściowy filtru modelującego; c) sygnał wyjściowy filtru modelującego; d) wgm sygnału wejściowego filtru innowacyjnego; e) wgm sygnału wejściowego filtru modelującego; I ) wgm sygnału wyjściowego filtru modelującego

[xcentrj = cntr(x);

[e.r.rhol = leemorf(xcentr,M.lambda); inp=randn(T,1);

[inpcentrj ³ cntr(inp):

[einp,rinp,rhoinp] = leemorf(inpeentr,N,lambda);

[inpstandj = stnd(einp(:.N));

(y.ee.rr] = morflee(inpstand,rho);

[ce,cce,nccei = korel(e(:,1), K) ?

(einp,ccinp.nccinp] =* korel(inpstand,K);

[cee.ccee.nccee) = korel(ee1),K);

(We.weI = wgmx(e(:,1));

(Winp.winp] ■ wgmx{inpstand);

(Wee.wee) - wgmx(ee(:.l));

me-max(e(:,1)); mee=max(ee(:,I)); nWe^amax(Wę); mWoe=max(Wee) ; subplot (2.3.1) ; plot (e (:, 1)/me) : grid; titleCa)'); subplot (2,3,2) ; plot (inpstand) ; grid; titleCb)'); subplot 12,3,3) ; plot (ee (: , 1)/mee) ; grid; titleCc)'); subplot (2,3,4) ; plot(we/pi.We/mWe); grid; titleCd)*); subplot (2,3,5) ; plot(winp/pi,Winp); grid; titleCe)'); subplot (2,3,6) ; plot (weo/pi . Wee/mWeel ; grid; titleCf)');

Wyniki symulacji przedstawia rys. 7.5.

PRZYKł.AD 7.9 Adaptacyjna estymacja widmowej gęstości mocy Algorytm adaptacyjnego filtru innowacyjnego wyznacza w każdej chwili czasu zbiór wartości współczynników Schura. znajomość których umożliwia wyznaczenie w każdej chwili czasu odpowiedzi impulsowej filtru Levinsona (z użyciem funkcji schur_lev.m) i transmitanćji tego filtru (z użyciem funkcji ampl.m) Znając zmienną w czasie transmitancję filtru, można wyznaczyć zmienny w czasie estymator Levinsona widmowej gęstości mocy szeregu czasowego (zgodnie z zależnością (2.184)). Omawiany przykład ilustruje taką adaptacyjną estymację wgm dla sygnału składającego się z trzech składowych sinusoidalnych o różnych częstotliwościach, pojawiających się z wzajemnym opóźnieniem 50 próbek (patrz rys. 7.6a)). Postać źródłowa /n-pliku P9 .m jest następująca: % P9.m Adaptacyjna estymacja widmowej gestosci mocy

% .................................................

% dlugosc sygnału

dlugosc funkcji autokowariancji * rząd filtru Lovin9ona

gancomptr,1.200.50.200,    100.200.0.05,0.30.0.8);

• cntr(x)j

% doklnracj* «,pol=»ym>ik» zopomin.ni.

for t“l:T

(AJ)    ³ achur_lev(rholee(c.:) l ;

for i»l:N aa(i)=A1(i.N); end

182

183