79319 skryptF

Rys. 7 6.

iMri FMEMTACJĄ ALGORYTMÓW CYFROWEJ FILTRACJI ORTOGONALNEJ

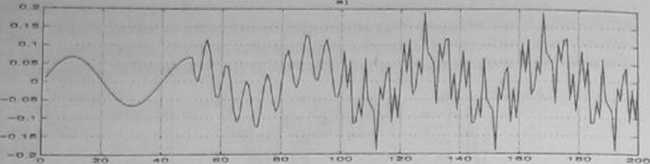
Wyniki symulacji w przykładzie 7 Q: a) sygnał składający się z trzech składowych sinusoidalnych o różnych częstotliwościach; b) zmienny w czasie estymator widmowej gęstości mocy sygnału

for i=N+l:T aa(i)=0: end (HAl.wH) = ampl(aa);

H22=HA1 .* HA1;

for i=l:length(H22) H_J22 (i) =1/H22 (i) ; end for 1=1:length(HA1); H(t.i)=HA1(i); end for i=l:length(H_22); W(t,i)=H_22(i); end

end

subplot (2,1,1); plot (xs) ; grid: titleCa)*):

subplot(2,1,2)z mesh(W/max(max(W))); view{100.35); title(*b)');

Wyniki symulacji przedstawia rys 7.6.

PRZYKł U) 7.10 Adaptacyjne odszumianie szerc

Przykład ilustruje zastosowanie omówionego w punkcie 6.6 algorytmu adaptacyjnej łącznej estymacji dwóch związanych ze sobą statystycznie szeregów czasou-ych, dla przypadku odszumiania sygnałów Na wejścia filtru estymacyj-nego (funkcja joint.m implementująca algorytm omówiony w punkcie 6.6) podawane są szeregi czasowe, scentrowany sygnał xcentr stanowiący sumę sygnału użytecznego (składowa harmoniczna) i szumu noise oraz scenlro-wany szereg czasowy noisecentr skorelowany z sygnałem xcentr Funkcja joint zwraca estymator sygnału użytecznego. Postać źródłowa m pliku PI0 . m jest następująca:

% PIO.m Adaptacyjne odszumianie sygnałów

\ ...........................................

elear;

RYS. 7.7

J57MULACJE MGOnYTMÓW r.»cn™.,.______

-—--_{ortoqomai mc} ,

'    -nuoo«l „_y,_nalu

'.laracja rzędu filtru

T-400;    ,

N*20:

lambdami;    .

!r*°i

noise=attn*noi(1:T); noiael=«noi (T/20+1 :T+T/20) •

(noisecentr] - entrtnoiaei); x»xl+noise;

(xcentrl = cntr(x);

«*xUT/2^:Tn^entr'^n0l"^C*^ntr,N' ’^ambdi° ‘

xn=xcentr(T/2+l:T);

ee»ex(T/2+l:T,N+l);

[Wxx.wxxł ~ wgmxlxx>_;

(Wxn,wxn) = wqmx(xn);

(W*«.wee) „ vgmx(ee)_;

subpl°^t(2.3.^1>; plot (xx/max (xx) ) ; grid; titleCalM.

subpiot(J:!:*!; piot!^x!ee!!; lllt tuie!’c!*!^;

Wyniki symulacji przedstawia rys. 7.7.

A

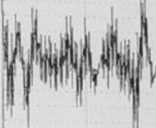
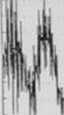
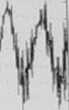
X

Wyniki symulacji w przykładzie 7.10 a) sygnał oryginalny; b) sygnał zaszumiony; c) sygnał odszumiony; d) wgm sygnału oryginalnego; e) wgm sygnahi zaszumionego; f) wgm sygnału

odszumionego

Implementacja algorytmów filtracji ortogonalnej w postaci m-PLiKów

184

liitlillii

Implementacja algorytmów cyfrowej filtracji ortogonalnej_________

7.2.

Implementacja algorytmów filtracji ortogonalnej w postaci m-plików

W niniejszym podrozdziale zostały zamieszczone (w kolejności alfabetycznej) implementacje algorytmów ortogonalnej filtracji cyfrowej (wraz z algorytmami pomocniczymi) w postaci funkcji (m-plików) dla środowiska MAT LAB 4.2. Funkcje te zostały wykorzystane w przykładach z podrozdziału 7.2. przedstawiających wyniki symulacji stanowiące ilustrację działania algorytmów omawianych w książce.

Funkcja ampl.m wyznacza charakterystykę amplitudową filtru na podstawie jego odpowiedzi impulsowej.

function tH,w) = ampl(h)

\ Wyznaczanie charakterystyki amplitudowej z odp. impulsowej

% ..............................................................

\ h ® wektor próbek odpowiedzi impulsowej filtru li H = wektor próbek charakterystyki amplitudowej filtru li w =- wektor argumentów funkcji H *

Hl*Cft(h);

Habs°abs(HI); nH=length(Habs);

H*Habs(1:1:nH/2}; nH*length(H); n=(1s1;nH)i w*pi/nH*n;

Funkcja cholesky.m stanowi implementację algorytmu faktoryzacji Chole-skiego macierzy kowariancyjnej Toeplitza z wykorzystaniem algorytmu I cvin-sona, omówionego w punkcie 2.2.3. Wyznacza ona dolnotrójkątne faktory Cho-leskiego macierzy Toeplitza i macierzy odwrotnej na podstawie górnotrójkątnej macierzy odpowiedzi impulsowych filtru Levinsona. Dokonuje porównania macierzy Toeplitza w postaci oryginalnej i sfaktoryzowanej oraz macierzy odwrotnej (wyznaczanej procedurą MATLABa) i jej postaci sfaktoryzowanej. Wylicza błąd średnlokwadratowy odstępstw tych macierzy.

function (P,Pinv.Cfact,Cinvfact) * cholesky(A)

% Faktoryzacja Choloskiego macierzy kowariancji i macierzy odwrotnej

* ..............................................................

% A = macierz qornotrojkatna odp. imp. filtru Levinaona ^ P » dolnotrojkatny faktor Choleskiego macierzy CM 1)

Pinv ■ dolnotrojkatny faktor Choleskiego macierzy C \ Cfact «* Pinv^,łPinv % Clnvfact ■ P*P'

\ p • dolnotrojkatny faktor Choleskiego macierzy CM-lJ % Pinv = dolnotrojkatny faktor Choleskiego macierzy C \

lm.nl-sizetA);

for i=l:n if i==l

for j=l:n P<j,i)=A(j,n); end else

for j ■= 1: i -1 P(j,i)»0; end

for j=i;n P(j,i)=A(j-i+l,n+l-ił; end

end

end

Pinv=inv{p);

Cfact=Pinv *Pinv;

Cinvfact=P*P* ;

Funkcja cntr.m dokonuje operacji centrowania sygnału zadanego w postaci naboru próbek; wynikiem jest nabór próbek sygnału o zerowej wartości śred niej.

function [yj » cntr(x)

% Centrowanie sygnału

% ............................................

ł x = wektor próbek sygnału

% y = wektor próbek sygnału scentrowanego

%

T=length(x); m=0;

for t»l:T m=m+x(t); end

m=m/T;

y=x-m;

Funkcja gen.m generuje wąskopasmowy sygnał przypadkowy, na drodze filtracji przypadkowego sygnału szerokopasmowego z użyciem filtru środkowo-przepustowego (okno Blackmana).

function (xl « gen(T.dl.gl.d2.g2>

Generacja przypadkowego sygnału wąskopasmowego

% .................................................

% T - liczba próbek generowanego sygnału % dl, gl » częstotliwości dolnego Dnsmn przejściowego % d2, q2 = czestotIlości gorneqo pasma przejściowego > x o wektor próbek generowanego sygnału %

dlpi-dl*pi; glpi=*gl*pi; d2pi-d2«pi; g2pi*«2*pi; pasmo^min { (glpi-dlpi),(g2pi-d2pi)); dlfil°ceil(11*pi/pasmo)♦li n«[0:1:dl Cii -1J; czdol=(dlpi+glpi)/2; czgor = (d2pi-*-q2pi) /2 ; u«n • (dlfil- l)/2«-eps; odpdol =»3in (czdol *u) ./(pi*u) r odpgor^sin(czgor*u)./(pi*u) i Odp-odpgor•odpdol: okno*(blackman(dlfil)) ' * h«odp.‘okno;

186