39655 PC043360

Rozdział:h Funkcje jednej zmiennej

TWfKJtDZEME 3.35.

Niech funkcja / będzie dwukrotnie różniczkowalna w sposób ciągły na dziale (o. b). Wtedy:

a)    funkcja/jest wypukła na (a.b) wtedy i tylko wtedy, gdy f"(x) > \ każdego .te (a.b),

b)    funkcja / jest wklęsła na (a.b) wtedy i tylko wtedy, gdy f”(x) <(J każdego x e (a.b),

c)    jeśli dla każdego x e (a.b) zachodzi f'(x) > 0 (odpowiednio f(x) < to funkcja /jest ściśle wypukła (odpowiednio ściśle wklęsła) na (a, b).

Implikacja odwrotna do podanej w punkcie c) twierdzenia 3.35 jest fafezyj funkcja f(x) = .i⁴, x € /?, jest ściśle wypukła na R. natomiast /" nie zaws jest dodatnia.

Twierdzenie 3.36.

Załóżmy, że funkcja / jest dwukrotnie różniczkowalna w sposób ciągły w pet nym otoczeniu punktu .ty. Wtedy:

a)    jeśli (xo,/(xq)) jest punktem przegięcia wykresu /, to /"(jto) = 0,

b)    jeśli istnieje takie r > 0, że na jednym z przedziałów (xo~r,xo), m\xo+r) mamy /"(*) < 0, a na drugim f"(x) > 0, to (x₀,f(xo)) jest punktem pi®, gięcia wykresu /.

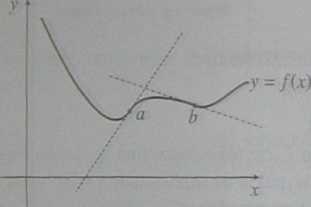
Rys. 3.6. Punkty a,b są punktami przegięcia wykresu funkcji / Źródło: opracowanie własne

Implikacja odwrotna do podanej w punkcie a) twierdzenia 3.36 nie jest prawdziwa. Druga pochodna funkcji f(x) - x⁴ w punkcie jc = 0 jest równa zeru, natomiast punkt (0,0) nie jest punktem przegięcia wykresu tej funkcji.

Przykład 347.

Podamy przedziały wypukłości i wklęsłości oraz wyznaczymy punkt przegięcia wykres¹ funkcji /(x) = c~^xt/2:

Ponieważ /"(jc) = (z²-1 )f(x) oraz f(x) > 0 dla wszystkich xeR. więc/"(r)>0 wtedy i tylko wtedy, gdy |x| > 1 oraz /"(jc) < 0 wtedy i tylko wtedy, gdy W < 1.

Funkcja / jest zatem (ściśle) wypukła na każdym z przedziałów: (-oo,-l), (1.®) natomiast (ściśle) wklęsła na przedziale (—1,1). Punkty przegięcia jej wykresu imr odcięte -l;, 1 i jednakowe rzędne równe e'^l/2.

Badanie przebiegu zmienności funkcji najczęściej odbywa się według następującego schematu:

a)    Obliczenie najważniejszych granic funkcji, w szczególności na końcach przedziałów określoności oraz w punktach nieciągłości. Zbadanie istnienia asymptot.

b)    Analiza pierwszej pochodnej: wyznaczenie przedziałów monotoniczności i ekstremów funkcji.

c)    Analiza drugiej pochodnej: wyznaczenie przedziałów, w których funkcja jest wklęsła i wypukła oraz punktów przegięcia wykresu funkcji.

Przykład 3.48.

Zbadamy przebieg zmienności funkcji

f(x) — xe^l/x, x# 0.

Ważniejsze granice to:

lim /(x) = —oo,    lim/(x) = OO.

lim /(x) = 0.

x-*o-

lim/(x) = 0, lim f(x) = lim —— = lim e^,/x =oo. X—o*    I—O* l/x    X—0*

Ostatnią granicę obliczyliśmy, korzystając z reguły de 1'Hospitala. Wykres funkcji ma więc asymptotę pionową prawostronną — jest nią prosta o równaniu x = 0. Poszukajmy asymptot ukośnych. W —oo mamy

Prosta o równaniu y = .t +- 1 jest więc asymptotą w -oo. Można larwo pokazać, że jest ona także asymptotą w oo.

Funkcja / jest różniczkowalna. a jej pochodna wyraża się wzorem

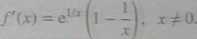
Proste rachunki prowadzą do wniosku, iż

f{x) < 0 <=> 0 < x < 1, /'(x) > 0 <=> x < 0 v x > 1.

Funkcja jest więc malejąca na przedziale (0.1). a rosnąca na każdym z przedziałów (-co, 0) oraz (1. oo). Druga pochodna funkcji / ma postać

/"(x) = ~^q^Vx, x#0

i pizyjmuje wartości dodatnie dla x > 0, ujemne zaś dla x < 0. Funkcja jest więc ścisłe wypukła na przedziale (0, co), ściśle wklęsła na przedziale (-oo,0). Wykres funkcji przedstawia rys. 3.7.

13.1