41711 img031 (43)

36

algorytmów wykorzystujących aproksymację funkcji /(•) występującej w danym równaniu (3.1), a w tym szeroko stosowaną aproksymację odcinkowo-liniową [6], czy też metody gradientowe będące tematem dalszych rozdziałów. Algorytmy wykorzystujące aproksymację odcinkowo-liniową należą przy tym do algorytmów przybliżonego rozwiązywania realizujących zadanie w skończonej liczbie kroków. Do szeroko wykorzystywanych metod należą też metody stosujące przeszukiwanie statystyczne [23],

Osobna grupa metod dotyczy zadania przybliżonego rozwiązywania równań wielomianowych, to znaczy równań postaci

(3.2)

a_n-x" + a_n_j • x" ¹ +... + a_x • x + a₀ = 0 ,

gdzie x e R oraz a₀, a\, •••,«„£ R. Jak wiadomo z wykładów z algebry - teoria Galois [1], wzory dokładne na pierwiastki równań wielomianowych otrzymane jako wynik skończonej liczby działań algebraicznych dodawania, odejmowania, mnożenia i dzielenia oraz operacji pierwiastkowania stosowanych do współczynników wielomianu można przedstawić w przypadku ogólnym tylko dla równań stopnia n < 4 . Dla równań wielomianowych dowolnego stopnia istnieją metody ich przybliżonego rozwiązywania specjalnie dla nich opracowane. Wymienić' tu należy przede wszystkim metodę iteracyjną Laguerre’a czy też metodę Baristowa [7, 8],

Dla równań wielomianowych o współczynnikach rzeczywistych opracowano też metody oszacowania liczby pierwiastków rzeczywistych oraz metody pozwalające na wstępną lokalizację pierwiastków [7, 8, 21].

3.1.1. Metoda bisekcji - metoda połowienia [7, 8,19]

Zakłada się, że występująca w równaniu (3.1) funkcja/(-) jest ciągła na zadanym przedziale [a, b] i spełnia w punktach krańcowych warunek

(3.3)

A zatem w przedziale (a, b) znajduje się co najmniej jeden pierwiastek danego równania (3.1). Zadanie polega na wyznaczeniu przybliżonej wartości jednego z pierwiastków równania w zadanym przedziale (a, b). W metodzie bisekcji obliczenia przebiegają według następującego algorytmu.

Zadane zostają liczby dodatnie 5 i e określające wymaganą w zadaniu obliczeniowym dokładność wyznaczenia przybliżonej wartości pierwiastka. Odnośnie do liczb 8 i e zakłada się, że mają wartości większe od błędu zaokrągleń wynikającego ze skończonej precyzji zapisu liczb w komputerze.

Krok 1

Przedział [a, b] jest dzielony na połowy punktem

(3.4]

a + b

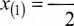
Jeżeli J{^xO)) ⁼ to ^x(i) jest pierwiastkiem danego równania (3.1). W przeciwnym razie sprawdza się, czy spełnione są następujące dwa warunki: