50828 skanuj0293 (3)

cia stosuje się te same wzory, co dla kół walcowych prostych dla przekroju normalnego, a następnie oblicza się odpowiednie wartości w przekroju czołowym.

PRZYKŁAD 11.8. Obliczyć podstawowe wymiary kola walcowego skośnego o liczbie zębów z = 18, module normalnym m — 6 mm i kącie pochylenia linii zęba /? = 10°.

Rozwiązanie

Podziałka normalna: p = n m = n-6 = 18,84 mm

Moduł czołowy: m_t =

cos fi 0,9848

6,09 mm

18,84

= 19,13 mm

Podziałka czołowa: p. = -—

cos fi    0,9848

Wysokość głowy zęba: h_a — m = 6 mm Wysokość stopy zęba: h_f = l,25m = 1,25-6 = 7,5 mm Wysokość zęba: h = 2,25m = 2,25 • 6 = 13,5 mm m • z 6 18

Średnica podziałowa: d —-=-« 109,667 mm « 109,7 mm

cos fi 0,9848

(z    \    / 18

Średnica wierzchołków: d. = ml-+2 = 6 -+ 2 1 =

\cos fi    )    \ 0,9848

= 121,667 mm « 121,7 mm

Średnica podstaw: d_f — m

18

cos/?

—2,5 = 6

0,9848

-2,5

94,667 mm « 94,7 mm.

PRZYKŁAD 11.9. Ustalić graniczną liczbę zębów dla kół walcowych skośnych o kącie przyporu a₀ = 20°, w których będą stosowane zęby o kącie fi = 20°.

Rozwiązanie

Zakładamy, że podcięcie zarysu zębów jest niedopuszczalne z_gp = Zg ■ cos³ fi = 17 0,9397³ « 14,1 Przyjmujemy z_g„ = 14.

Gdy dopuścimy minimalne podcięcie zarysu, otrzymamy z'_gfi = z'g-cos³/? = 14• 0,9397³ « 11,6

Przyjmujemy z'_g0 = 12.

Obliczanie wytrzymałości zębów skośnych. Rozkład sił działających w przekładni z kołami o zębach skośnych jest przedstawiony na rys. 11.20.

Podobnie jak w przekładniach z kołami o zębach prostych, siła obwodowa F, wynikająca z przenoszonego momentu obrotowego, jest siłą stanowiącą podstawę do obliczeń, natomiast siłą obciążającą zęby jest siła międzyzębna F_z.

Zęby skośne są zginane siłą F_n, a o wartości nacisków powierzchniowych decyduje siła F_z. Jak wynika z rys. 11.20, w zależności od siły obwodowej F można obliczyć

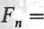
(11.68)

F

cos(3

293