52664 P3041064

lii

gdzie:

, l,,

. fd

/ _ moment bezwładności przekroju zastępczego składające.,,

' się _z przekroju żebra pionowego i części współpracują! b blachy poziomej.

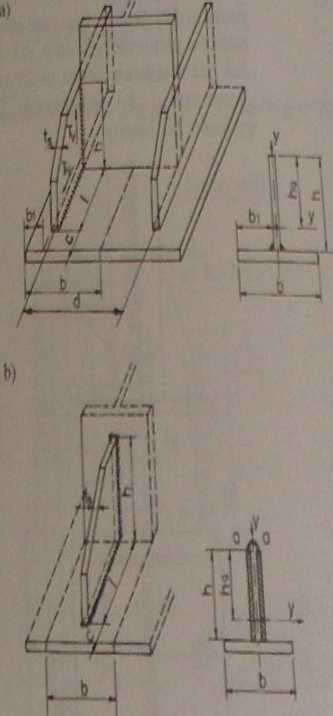
Ryi.7.65. Model obciążenia żeber i blach trapezowych stopy słupa

I il

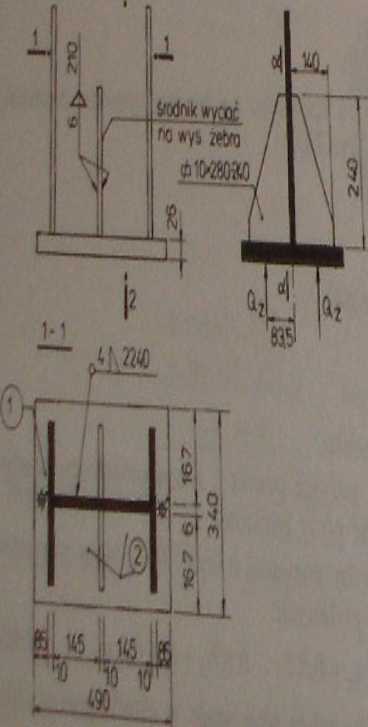
Ib Przykład 7.16

Zaprojektować żebra usztywniające stopą słupa obciążonego siłą N_c= 1100 KN.

Elementy stopy ze stali St38Y, Wytrzymałość obliczeniowa na docisk fundamentu Rw=7MPa.

^Rozwiązanie

| Zaprojektowano blachą poziomą Ml o grubości 26 mm (rys.7.66).

Średni opór fundamentu p=6,6 MPa.

2. Zebra usztywniające Szerokość streiy pod obciążeniem:

b*14,5+1,0=155cm

Siła ł moment zginający działający "• Jedno *<**<>

Qz= 16.7 155 0.66 • 170.8 kN M * 170,8 0.167 05' 1426SkNm Współpracująca część płyty poziome) o 0.6 167-100 cm. Położenie osi y, czyli * wynosi:

/u.*-^{24 1} <**-♦**!>

* 10 2,6 ♦ 24 1

Moment zginający przekroju zastępczego:

11.3* 16.3 cm

. 1 24³ ₄*¹⁴

1 <10.3 - 12Y* ♦ 10 2,6 6.4* - 2475 cm⁴

Naprężenia:

°^m'wi ^1M W-93-9W* <e*’S^f"^7,MP,‘

Nie obliczono nośności zredukowanej ze wzglądu na nłewWMą wartości napręża* Zasady projektowania Wach trapezowych stop slupów dwugałąziowych tą taka same jak pojedynczych żeber ueztywnśe*cych stopy trzonów petnoiciennych.

J4MB_

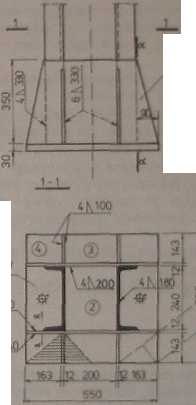
(f o Przykład 7.17

Zaprojektować żebra usztywniające oraz Wachy trapezowe stopy słupa obciążonego alą osiową *-1610 kN flw= 5 MPa Elementy stopy ze sta* SOSY

^Rozwiązanie

Zaprojektowano blachę poziomą 550*550x30 (rys-7.67).

1. ObNczenie żeber pionowych:

0/ - 0,5 * 27,5 14,3 0.5 • 08,3 kN

14= 08.3 ² 14.3 -9.37 kNm 3

Szerokość współpracująca b = Q,6l P-0.6 14.3-8,6 cm

. ~ 27 1 16.5 -85 3 1.5 _m99tLKm^ ^{= 30}' 27 1 *8,6 3 ^a22-^8Cm

Ryt. 7.67

8.6 3(7,4* t,S>*

1 27* ⁺ 12

27 1 (22,6 -135)* ^a 5920 cm⁴

9.37 22.6 10* 5020

36 MPa. t 1° ■ 36 MPa

Pominięto sprawdzanie nośności zredukowanej.

2. Blachy trapezowe Siła i moment zginający przekroju a~a :

«7“ *2 ^0,5 M*l%},75 kN

445