65535

gdzie:

M(x) -funkcja momentu zginającego,

E -moduł Younga,

J -moment bezwładności przekroju belki względem osi obojętnej, przechodzącej przez środek ciężkości i prostopadły do płaszczyzny zginania.

Funkcje momentów zginających dla przedziałów zmienności argumentu x mają postać: dla 0<x,<a,

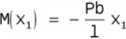
(2)

(3)

dla a < x₂ < 1 Pb

M(X₂) = - — x₂ + P|x₂ - a]

Podstawiając funkcje momentów zginających do równania różniczkowego osi odkształconej belki (1) otrzymamy odpowiednie równania różniczkowe:

EJ

d V,

dx*

Pb

dxj

1

(4)

X, * X; - a

Po pierwszym scałkowaniu obu równań otrzymamy

(5)

EJ

d

dx.

pb

21

X? + C,

(6)

dx,

Pb ; Rx, - a — x‘ * ——— t C,

(7)

21 ²    2

a po drugim

Pb ,

EJy_t = - — xj + C_lXl + D,

Pb ₃

EJy? = - ^    +

P(x₂ - a)

+ C,X, + D,

(8)

(9)

Stałe całkowania Cg, C₂, D,, D₂ wyznaczymy z następujących warunków brzegowych:

l)^x,	= G	O II >> it
*1	= X2	= a =>
2)
3)^X»	= x2	= a => y
4)V	1 3	h--\

dy₂

dx₂

dy, ₌

dXj

i = y_2>

Podstawiając warunki brzegowe do równań (6), (7), (8), (9) otrzymujemy wzory na linię ugięcia w dowolnym przekroju przedziału pierwszego i dntgiego belki: