55173 Str062 (7)

62

62

£0=1,O±5%.

*	= ze~ 2,	p’ =	4
Z i*	= ze~ 1,	p** =
Początkowy „ wariant & £	=	p =
*** ze	= Ze+ 1,	p *** =
**** ze	- z E+ 2,	p **•*=	4

F_n=2ltfT₂Jd_v

F_r2=F_l2tga/cosp-

Fa2=F_t2tgP.

±invao ^+mva (z,±z₂)

zębatego

*5. = A\-t-X,=

3. OBLICZANIE £„ I KOREKTA PARAMETRÓW PRZEKŁADNI (tylko dla /S >0°)

3.1. Zaleca się korzystać z przekładni o całkowitej liczbie poskokowego wskaźnika zazębienia

^£0⁼ 1.0; = 2,0; ...

Dla wspólności z p. 2 zaleca się przyjmować

Poskokowy wskaźnik zazębienia s'p = b₂ sin/S/(nm).

3.2. Doprowadzenie obliczonej wg p. 3.1 wartości Ep do wartości zalecanej Ep = 1,0 wykonuje się:

3.2.1.    Wgp. 1.5, 1.6 (5.3.1) prowadzi się dobór

parametrów z_E i p przy założeniach: ze=z_e± 1,    zz=zz±2.

3.2.2.    Dla każdego wariantu oblicza się Ep.

3.2.3.    Otrzymane wyniki wprowadza się do tablicy

*** _

**** _

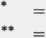
3.2.4.    Z otrzymanego szeregu Ep, dotrzymując warunku (8°^ p $ 22°), dobiera się wartość najbardziej zbliżoną do Ep ⁼ 1,0 wgp. 3.1. Jeżeli czynności p. (3.2.1...3.2.3) nie skutkują, to jest możliwa zmiana m„ z powrotem do p. 1.4.

3.2.5.    Tę wartość doprowadza się do Ep wgp. 3.1 przez zmianę szerokości koła b ₂. Nowa szerokość koła ó₂=(£_p7Tm_D)/sin/3, mm.

(dokładność obliczeń - jeden znak po przecinku). b, = b₂+ (3...5), mm (£>, - liczba całkowita). (Dla wykonania warunku *** 5.2.1 p. 2.7 dopuszcza się korektę twardości kół zębatych i naprężeń dopuszczalnych a®, (5.2 p. 2)).

3.2.6. Wykonuje się obliczenia (5.3.1 p. 1.7...1.9).

4. SPRAWDZANIE OBLICZENIOWYCH NAPRĘŻEŃ

GNĄCYCH

4.1.    Współczynnik międzyzębnego obciążenia dynamicznego przy zginaniu zęba k_F$ = f (i?, klasa dokładności, twardość zębów) (tabl. 5.3.14).

4.2.    Współczynnik nierównomiemości rozkładu obciążenia wzlędem linii styku k_Fp = f (HB, rozmieszczenie kół względem łożysk, lAw ) (rys. 5.3.3c,d).

4.3.    Współczynnik uwzględniający nierównomiemość rozkładu obciążenia między parami zębów w zazębieniu k_Fa = f (i?, klasa dokładności):

-    dla zębów prostych k_Fa = 1,0;

-    dla zębów skośnych k_Fa (tabl. 5.3.12).

4.4.    Jednostkowa obwodowa siła obliczeniowa przy zginaniu, N/mm W_Ft=F_tk_Fp k_Fp k_Fak_A/b₂.

4.5.    Ekwiwalentna liczba zębów:

-    dla zębów prostych z,_(2)eq=zi₍₂₎;

-    dla zębów skośnych z_l(2)eq=z_s(2)/cos³p.

4.6.    Współczynnik kształtu zębów zębnika i koła zębatego Y_rai(2)=f(zi(2)eq,^i(2)) (*i<2)=0) (rys. 5.3.5). Obliczenia wykonuje się dla koła z pary „zębnik -koło zębate", dla którego jest mniejszy stosunek ⁽JfP_](2)/YfSi(2)-

4.7. Naprężenia obliczeniowe gnące, MPa

°fi(2)⁼    i(2) Yp W_Ft/m < (J_FP 1(2),

gdzie Yp - współczynnik kąta pochylenia linii zęba:

-    dla zębów prostych Yp =1,0;

-    dla zębów skośnych Y„ =l-Ep p°/\40°. Jeżeli Ep >1,0 , do równania podstawia się Ep= 1,0. Jeżeli/S >30°, do równania podstawia się p = 30°.

5. SPRAWDZANIE WYTRZYMAŁOŚCI ZĘBÓW PRZY PRZECIĄŻENIACH

5.1.    Naprężenia stykowe przy przeciążeniach, MPa

ćt// max ⁼    / Tmax/ Tnom' n Ofip rnax ](2) ■

5.2.    Naprężenia gnące przy przeciążeniach, MPa

max 1(2) Of 1(2)( kniax^/ 7nom) $ (TfP max 1(2) *

6. SIŁY DZIAŁAJĄCE W ZAZĘBIENIU PRZEKŁADNI

6.1. Moment rzeczywisty na wale wyjściowym, Nm

^T2tz⁼T₂ Un/U.

6.2. Siły obwodowe, N F₍₁=2 10³7’,Ą/_w1;

6.3.    Siły promieniowe, N F_r i =i^rntga/cosjS;

6.4.    Siły poosiowe, N F_al=F_t}tgP;

(a =20°)

7. OBLICZANIE GEOMETRYCZNE KÓŁ WALCOWYCH O ZĘBACH PROSTYCH KORYGOWANYCH DANE WEJŚCIOWE: m, z,, z₂, a = 20°.

7.1.    Odległość osi podziałowa, mm o = 0,5m (z,±z₂), gdzie ± - (górny znak) - dla zazębienia zewnętrznego;

- (dolny znak) - dla zazębienia wewnętrznego.

7.2.    Odległość osi rzeczywista o^nim wg PN (tabl. 5.3.3) a_w>a.

Otrzymane w 5.2.1 p. 1.7 liczby zębów należy przyjąć w taki sposób, żeby dla zazębienia:

-    zewnętrznego

0,5m(z2+z,+2)<a_w; 0,5m(z₂+z_t+3)>a_w\

-    wewnętrznego

0,5m(z₂-zi)<a_w; 0,5m(z₂-zi+l)>a_w.

7.3.    Toczny kąt przyporu, st

a₀ = arccos [(o/a^jcosa],

7.4.    Suma współczynników przesunięcia zębnika i koła

— AiT ai —    ₀

¹    1    2 tg a

(dokładność obliczeń - 3 znaki po przecinku), gdzie inva = tga-a; inva₀=tga_o-a_o;

a, a o-w radianach.

Dla zazębienia zewnętrznego x_z > 0.

Dla zazębienia wewnętrznego x_L < 0.

7.5.    Pozorna odległość osi, mm

a'_w = a + x_zm„.

7.6.    Współczynnik zbliżenia osi (współczynnik skrócenia głowy zębów) y=(a_w-a_w)/m„.

7.7.    Wartości współczynników przesunięcia zębnika x, i koła zębatego x₂ przyjmuje się odwrotnie proporcjonalnie do liczby zębów x₂=x_lz_l/z₂.

Wtedy Xx=x_l+(x,z_I/z₂). Skąd x, = x_E/(l+z,/z₂); x₂=x_E-x_l. Zalecenia po podziału x_E - tabl. 12.2.4. (dokładność obliczeń - 3 znaki po przecinku).