57925 Untitled Scanned 31 (8)

i tej samej ramy różne układy podstawowe kierujemy się dążeniem do uproszczenia obliczeń wartości przemieszczeń d i A (por. p. 13.6.1-3-13.6.4). Postępując w przedstawiony sposób musimy pamiętać o tym, że tak obliczone wartości X_t nie są równe rzeczywistym reakcjom nadliczbowych więzów. Otrzymane wartości X_t wykorzystujemy do określenia wynikowych momentów zginających zgodnie ze wzorem (13.4).

Dysponując końcowym wykresem momentów zginających i ewentualnie sił poprzecznych i podłużnych (por. p. 9.7) oraz znanymi siłami zewnętrznymi obliczamy bez trudności rzeczywiste wartości reakcji dowolnych więzów zewnętrznych lub wewnętrznych.

Poprawność, pozornie niedopuszczalnego, równoczesnego posługiwania się różnymi układami podstawowymi tej samej konstrukcji możemy uzasadnić następująco. Dla różnych (prawidłowych) układów podstawowych rozpatrywanej ramy można uzyskać jeden i ten sam wykres momentów zginających stosując różne układy sił X_t o odpowiednich (określonych) wartościach (por. tzw. niewiadome grupowe, p. 13.6.5), np. rys. 13.33a, b oraz różne układy obciążeń zewnętrznych — np. rys. 13.34. Wprowadzone na rys. 13.34, w dwóch przypadkach, dodatkowe obciążenia zewnętrzne, w odniesieniu do układu rzeczywistego, wzajemnie znoszą się, można je więc w razie potrzeby dowolnie przyjmować. Skoro więc taki sam wykres momentów możemy otrzymać dla różnych układów podstawowych tej samej konstrukcji, to stosowanie jednego lub równocześnie kilku układów podstawowych jest praktycznie równoważne. Musimy tylko pamiętać o podanej uwadze dotyczącej reakcji nadliczbowych więzów.

Dalsze ogólne przykłady można znaleźć w pracy [20]. W przykładzie 13.3 ilustrujemy liczbowo omówione zagadnienie.

Przykład 13.3. Sporządzić wykres momentów dla ramy (rys. 13.35a).

Dla przedstawionej symetrycznej i symetrycznie obciążonej ramy przyjmiemy układ zastępczy jak na rys. 13.35b. Wykresy momentów od jednostkowych wartości nadliczbowych niewiadomych pokazano kolejno na rys. 13.35c, d, e. Dla obciążenia zewnętrznego przyjęto inny schemat (odpowiedni wykres M_p pokazany jest na rys. 13.35f). Dzięki tak dobranym układom podstawowym dla niewiadomych sił i obciążenia zewnętrznego otrzymamy:

<5l2 = <5₁3 = <5₂3=c521=<531=^:<532=^l_lJ = ^2p=^:0.

Równania kanoniczne przybiorą więc następującą postać:

<5,i *,=0;

(A)

>biiczymy teraz wartości <5 oraz A\

Sn X₂=0;

<533 X₃-\- ^_3p~0 .

2 ,3	7 3
—i^3; i	/^3;	<533
3	12
	2 ql^2 2 j	qf
A3pEJ—
	3 ?3	~ 18 ‘

3 ^:

Z łładn równań (A) widzimy, że tylko X₃^0. Podstawiając do trzeciego z tych równań wartości ir^K-iieszczeń i rozwiązując je otrzymamy:

—l³X₃ ——=0; 3    18

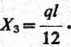
469