67111 z11 (9)

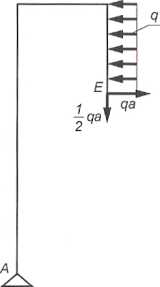
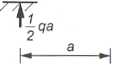
- pręt DF

ZM_f = qa-l-V_D-a = O —* V_D = ±qa, 52 X = Hp-qa = O —► H_F = qa_f

= o- iMgg.,_:

IK4

)]M_e    +    -■= !*§

TJ X = H_e~ qa = O — > H_e = qa,

y,r= V^fE c-ti

i |H('I BC

| )] M_b = -H_E'2a-qa’-a-H_F-a - V_Ea - V_c-a = O — V_c = -5qa,

I )] X = H_b - H_e - ąa - H_F = 0 —* H_B = 3qa,

! ^{Y = V}b ^{+ V}e ⁺ vf ⁺ vc ^{= 0} vb = ^Ą(ł^a-flflkl obliczeń przedstawiono na rys. 72.4.

mga: Pisanie równań sprawdzających na każdym etapie obliczeń jest pożą-łliinc, wręcz niezbędne. Unika się w ten sposób końcowego rozczarowania.

I W celu ustalenia uwagi sprawdzimy równowagę globalną ramy, tj. napiszemy na przykład równanie (por. rys. 72.4)

\ * Mr = —qcra - aa- — - 3qa-2a + qa- — + 5qa-a + qa-\a - \ qa'2a = 0 W* 2    2    2    2    2

i Pisanie warunku E K * 0 jest istotnie dobrym sprawdzeniem (z — dowolny leżący w płaszczyźnie ramy). Warunki E* * o, Er = 0 można wręcz IMibaczyć na rysunkach końcowych.

BĄDANIB 73

j Wyznaczyć reakcje więzów zewnętrznych i wewnętrznych w ramie pokazany! na rys. 73.1.

Mu/;wiązanie

I Przedstawiony typ konstrukcji ramowej nazywamy ramą ze ściągiem (pręty łamowe — ACD, BCE, ściąg — DE).

Z równań równowagi globalnej (rama jest zewnętrznie statycznie wyzna-

liflna):

Y,^ma ⁼ ~P’2a+Pa + V_B2a = 0,

y,^xf»A ^p“°-

obliczamy reakcje więzów zewnętrznych:

V* ■ ip, V_A » -P,    H_a = P.

u 2    <4    2 ’    ^