68279 p6 (7)

2. Modele matematyczne układów regulacji

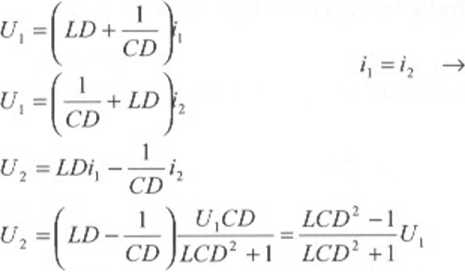
I =

G(D)= ' \^D\    ¹ gdzie T = JZc

TD² +1

V,

LD +

U_XCD LCD¹ +1

CD

Przykład 2.7

Zbudować model matematyczny U₂=f(fJ,), zakładając że C i R\ to połączenie

równoległe dwóch impedancji i R\.

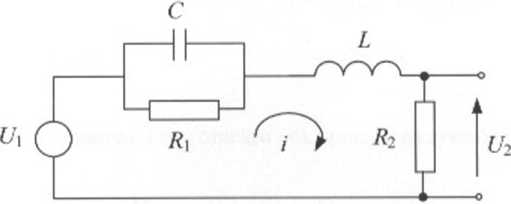
Rys. 2.7

R.

+ R.

-+ LD + R,

CD U₂ = R_}i

U₂ = JJ,

C£>

/?,£/,(— + *, ² V'Q '

/?, + ~ + LR_lD + -^ + R_lR₂

CD ¹ CD

CD

+ /?,

CD

u,

cr₂d + r_}r₂cd

23

1

R,+LD + LCR_XD +