57484 p5 (7)

2. Modele matematyczne układów regulacji

Przykład 2.5

Zbudować model matematyczny i wyznaczyć transmitancję operatorową G(D) dla układu mostkowego RC jak na rysunku 2.5. Spadki napięć są zawsze przeciwne do kierunku przepływy prądu.

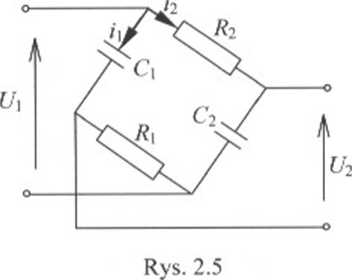
ĄC,D +1 U,C₂P R_lC₂D + \

^uA^D)=^-^

ii i i₂ podstawiamy do równania U2

^ u,V» 1 -t^d¹

^; {/,(£>) (T,D + \)(T₂D + \)

dla T\ = r₂

, . \-T²D² (l + TD^-TD) \-TD ~\+T²D² ~ (\ + TDX\ + TD) \ + td

T, = *,C,

T₂ = R₂C₂

Przykład 2.6

Zbudować model matematyczny i wyznaczyć transmitancję operatorową dla układu rysunku 2.6.

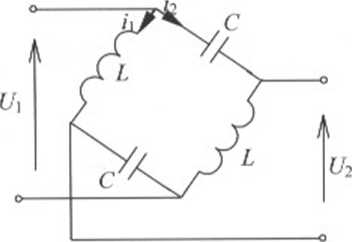
Rys. 2.6