68539 img480 (2)

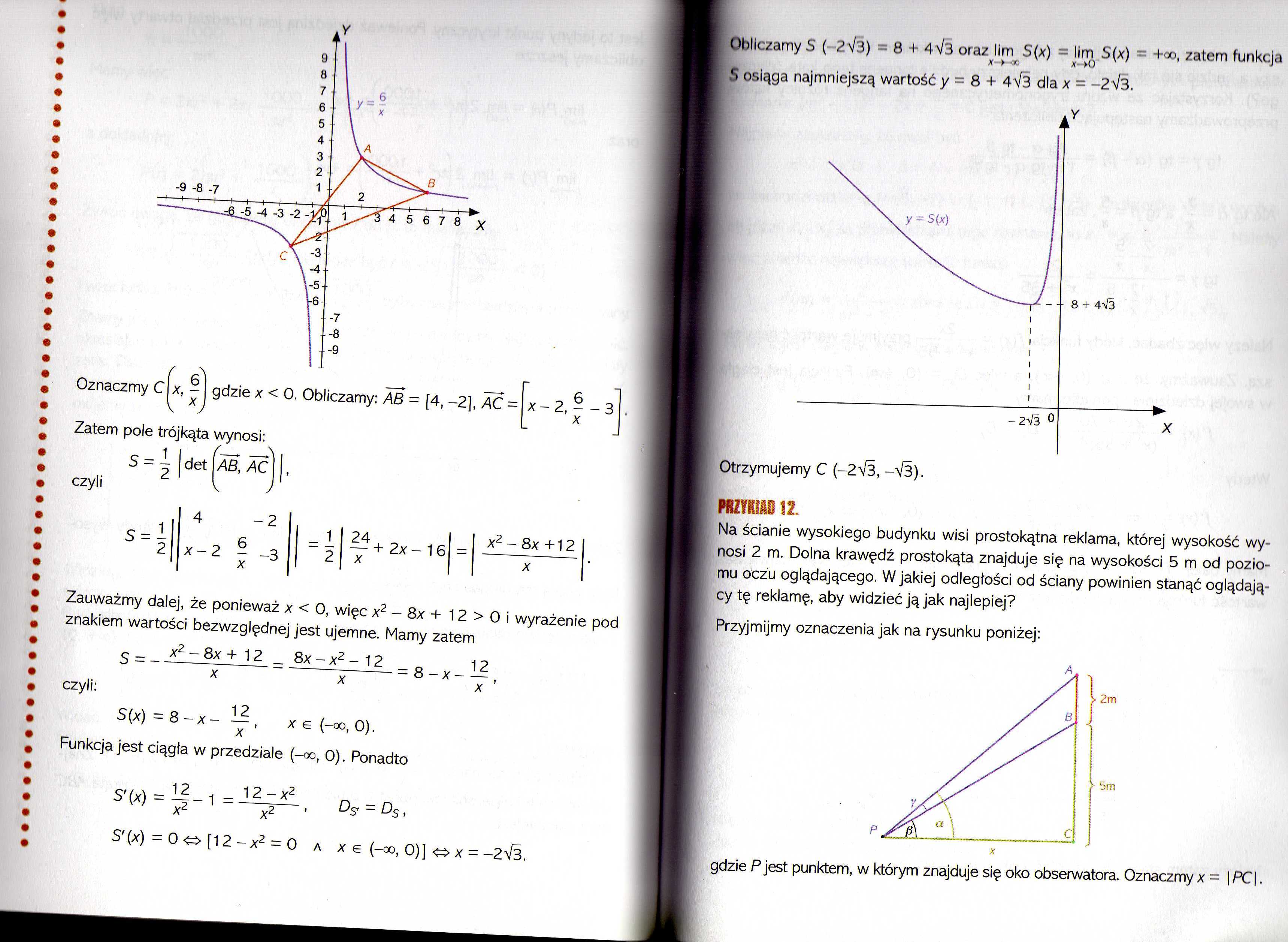
Zatem pole trójkąta wynosi:

S = |
	det	AB, AC
czyli		l )

Zauważmy dalej, że ponieważ x < O, więc x² — 8x + 12 > O i wyrażenie pod znakiem wartości bezwzględnej jest ujemne. Mamy zatem

c- x² - 8x + 1 2 _ 8x - x² - 1 2    „    12

---x---x-= 8-x--,

XX    _x

czyli:

S(x) = 8 — x - —, xe (-oo, O). x

Funkcja jest ciągła w przedziale (-oo, O). Ponadto

S'(x) =    1 =±Łr^xZ

X^    X‘

Dc? — Dc

2    ¹    ‘-'S’ - ^US >

S'(x) = O <=> [12 -X² = O a x G (-00, O)] ox = -2V3.

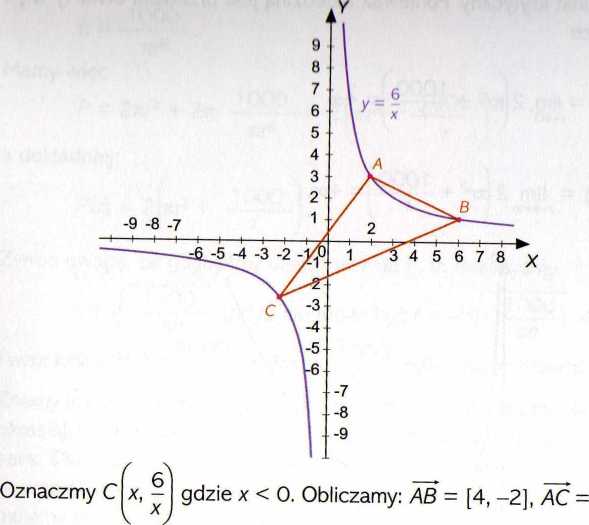
Obliczamy S ( 2^3) = 8 + 4^3 oraz lim S(x) = lim S(x) = ^+o0' ^zatem funkcja

x-*-oo    x-fO

‘i osiąga najmniejszą wartość y = 8 + 4V3 dla x = -2"v3.

Otrzymujemy C (-2^3, —V3).

PIZYRłAO 12.

Na ścianie wysokiego budynku wisi prostokątna reklama, której wysokość wynosi 2 m. Dolna krawędź prostokąta znajduje się na wysokości 5 m od poziomu oczu oglądającego. W jakiej odległości od ściany powinien stanąć oglądający tę reklamę, aby widzieć ją jak najlepiej?

Przyjmijmy oznaczenia jak na rysunku poniżej:

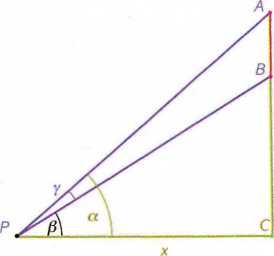
gdzie P jest punktem, w którym znajduje się oko obserwatora. Oznaczmy x = |PC|.

S

1_

2

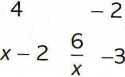
1_

2

— + 2x - 1 6

x² - 8x +12 x