71255 wyborcza odp002

2 Gazeta Edukacja

PonMddak 6 października 2006. Gazeta Wyborcza. www.wyboccza.pl

Partner

radiowy

RMr

MODEL ODPOWIEDZI Każda kropka {•) to 1 punkt.

Zadanie 1.

i • Zapisanie układu nierówności; (Znierówności trójkąta: surnu długości każdych dwóch boków trójkąta jest większa od długości trzeciego boku,)

3^{1 2}S>I²I | 3²|x|>5

ls+|i|>3

•• Rozwiązanie układu nierówności 1 zapisanie odpowiedzi is(-»;-2)u(2:8)

' Zadanie 2.

• •Wyznaczenie wszystkich wartości, dlaktóiychrównanie madwaróżnepierwiastki rzeczywiste.

me(-«;-1>/2)j(4r/2: +CO^

(RównaniekwudratoWBmadwaióżnu.pieinyiastluTzeczywLstc,gdy A>0, tu A-m³-32)

Wyznaczenie sumy S kwadratów pierwiastków w zależności od parametru m.

S=m’-16.

^ ² I,' - j’ + 2z,i, + - 2x, r, = (i, +x,)'-2x,i₎, (korzystamy zc wzorów Victc’a.)

•Ułożenieiruzwiązunierównania S=llm-34.

W-16=Mm—34 m, ²2, m, «9

•    Wybór rozwiązania spclniąjącego warunki zadania i sformulowanieodpowiedzl m- 9 ! Zadanie 3.

•Wprowadzenie oznaczeń, analiza warunków zadania i podanie założeń. d-liczba uczniów, n>3

z-kwota do zaplaceniaprzypadającanajcdnego ucznia.

•    Ułożenie układu równań.

1 Ina—72

l(»-3)(²+4)=72

u Erzuksżlulcenie układu równań do równani² kwadratowego z niewiadomą n. n’-3n-54-0

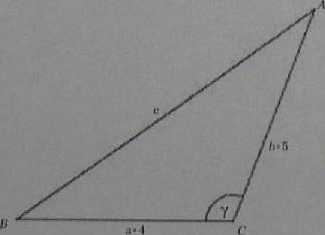
•Obliczenie siny. siny=0,8

• Zapisanie z twierdzenia kosinusów wzoru na c- długość boku AB. c=Ja³+/j³—2itbcosy

•Obliczenie cosy.

cosy =-0,6

(Wartość cosy. otrzymujemy z „jedynki trygonometrycznej" i faktu, że y jostiniarąkąlaroz-wartego.)

•Obliczenie e i podanie wyniku z wymaganym zaokrągleniem. c = 80,62 mm.

Zadanie 6.

• Natysowanieiysunku pomocniczego, wprowadzenie oznaczeń i analiza warunków zadania.

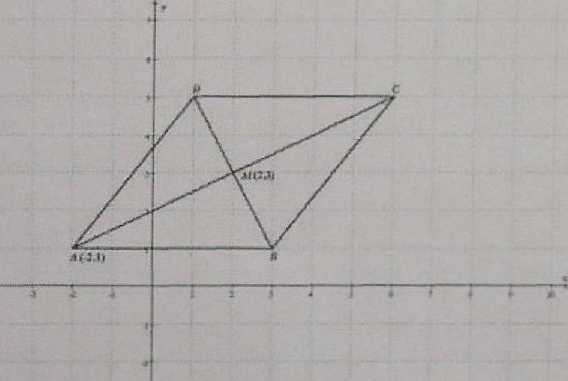
Punkt Af jest środkiem symetrii rombu i jednocześnie środkiem okręgu wpisanego w ten romb. • Obliczenie długości przekątnej AC \ac\-aJŚ 0WC|=2 |4M|)

www.wyborcza.pl wychodzi 24 godziny na dobę

• Rozwiązanieukładu równań, wybór rozwiązania spoinującego warunki zadania i sformulowa- • Obliczenie długości przekątnej BD. nie odpowiedzi.

n>9    |BD|=275 (ze wzoru na pole rombu)

| Na pi zzę wybrało się 9 uczniów.

• Obliczenie długości boku AR

(z twierdzenia Pitagorasa zastosowań ego do trójkąt² prostokątnego AMB)

•Obliczenie promienia rokręgu wpisanego w romb. r²2

(ze wzoru na polo rombu, r to potowa wysokości rombu)

Zadani* 5.

• Wprowadzanie oznaczeń, im przykład na rysunku, i zapisanie wzoru na pole P trójkąta zgodnie z przyjętymi oznacźonlaml.

!?/²■' ‘f ii Xr «■    £ '    ,    ......f \ i i ^

•Frzeltszlalceme lewej strony nierówności (x+y+7)|-+—f-Iz9 do postaci

KhHhMh)

• Przeprowadzenie dtiwodu w oparciu o nierówności z podpunktu a).

• Napisanie równania okręgu wpisanego w romb.

Zadanie 7.

•Ułożenie równania wynikającego z warunków zadania.

x?-2x'+9+2x»3 4x=-

|

|Przekształcenie lównunia 4x - ^ ~pi ^²2x+3 dopostsd x'-2x'-6x+l2=0. ••Rozwiązanierównania x'-2x^,-6xłl2-0.

x, - ~J6, x,« 2, X, - </ó

(y-Ir²-6x+12 -(<-2)-6(..-2)- (x-2 j(x'-6))

•ktybór rozwiązania spolnlująeogu warunki zadania. x-21ubx-s/Ś

1

Zadanie 4.

I Ste    x y - .

2

Przekształcenie nierówności 232 do postaci równoważnej i³ ♦ y³ a 2xy.

| • Przekształcenie nierówności x' + y' i 2xy do postaci (i-yfiO i sformułowanie wniosku i kończącego dowód.

3

P-Rośliny