78 6

TT"

7. PLANIMETRIA

Zadania do samodzielnego rozwiązania

Zadania zamknięte

1.    Obwód trójkąta równoramiennego jest równy 32 cm. Podstawa trójkąta jest o 1 cm dłuższa od Ramię trójkąta ma długość:

A. 11 cm    B.    10 cm    C. I l-j cm    D. I0-| cm

2.    Liczby 8.15. .x są długościami boków trójkąta prostokątnego, gdy:

A. .v = 17    B. .r=/ióT    C. x- 17 lub .v = y/lól D..r = Ju lub* = |»

3.    Wysokość trójkąta równobocznego jest równa 2» 3. Obwód tego trójkąta wynosi:

A. 4    B.    3    C.12/3    D. 12

4.    Kąt między ramionami trójkąta równoramiennego ma miarę 4 razy mniejszą od miary kąta przy p-ic wic. Miary kątów tego trójkąta wynoszą:

A. 30*. 30'. 120*    B.    40*, 40*, 100*    C. 20*. 80*, 80*    D. 20*, 20*. 140*

5.    Stosunek miar kątów trójkąta jest równy 2:3:4. Wskaż miarę największego kąta tego truj) :'

A. 45*    B.    80*    C.I60*    D. 145*

6.    Dany jest prostokąt mający tłoki o długości 4 i 8. Środki boków prostokąta są wierzchołkami f le tego rombu jest równe:

II Nj planie w skali 1 : 100 działka w kształcie kwadratu ma pole równe 72 cm'. Oblicz długość przekąt-(iriatki. Wynik podaj w metrach.

14.    Oblicz pole równolcgłoboku o bokach długości 1 dm i 4 cm oraz kącie rozwartym o mierze 150*.

15.    W okrąg wpisano trójkąt ABC. taki że \<BAC| = 50* i | <ABC | = 70*. Przez wierzchołek C poprowadzo-> styczną do okręgu przecinającą przedłużenie boku Ali w punkcie l). Oblicz miary kątów trójkąta BCD.

16.    Długość średnicy koła samochodu wynosi 16 cali (l cal = 2.54 cm). Oblicz, ile obrotów w ciągu 20 mi-• wykona to koło. gdy samochód jedzie z prędkością 90 Zakładamy, że 71 - 3.14.

17.    Stosunek długości przekątnych rombu, którego bok ma długość 8 cm. jest równy 4 : 3. Oblicz pole lepi rombu. .

*

Zadania otwarte rozszerzonej odpowiedzi

II Obwód trójkąta równoramiennego jest równy 250. Wiedząc, że ramię tworzy z podstawą taki kąt er, że tso ^-.oblicz pole trójkąta.

1t. Podstawa trójkąta ABC ma długość 12. Kąty przy podstawie mają miary 30* i 45*. Oblicz pole i obwód

tego trójkąta.

23. / wierzchołków prostokąta poprowadzono proste prostopadłe do jego przekątnej. Proste te dzielą . • jtna na trzy równe części, każda o długości 5 cm. Oblicz pole i obwód tego prostokąta.

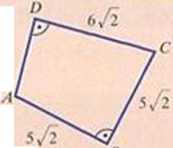
II. Oblicz obwód trójkąta równobocznego, którego wysokość ma długość 9. II Oblicz długość boku AD przedstaw ionego na rysunku czworokąta ARCD.

u

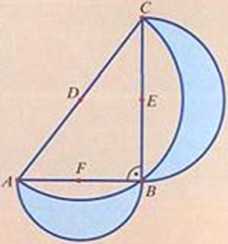
21. Na bokach trójkąta prostokątnego ABC w sposób pokazany na rysunku *rc \łOopółokręgi, których środkami są środki D. E. F boków tego trójką-ti Ot- a pole zamalowanej figury, wiedząc, że przyprostokątne trójkąta V* mają długości 6 cm i 8 cm.

21 Przekątna AC równolcgłoboku A BCD ma długość 6 cm. a przekątna BD jest prostopadła do boku AD tref kąt <Mry między przekątnymi ma miarę 60*. Oblicz pole i obwód równolcgłoboku.