85808 P1010688 (2)

10 I. STROPY

10 I. STROPY

tacyjne, dopiero wykonanie obwiedni momentów daje właściwy obraz, y/

Przy projektowaniu płyt dachowych nie ocieplonych zaleca się zbrojenie obl/czo zwiększyć o 15% ze względu na dodatkowe naprężenia spowodowane wpływem H temperatury.

Płyty ciągle można obliczyć również metodą plastycznego wyrównania momentó jeżeli

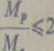
B

oraz jeżeli spełnione są następujące warunki:

-    zbrojenie elementów wykonane jest ze stali klasy A*0 do A-UI

-    wymiary przekroju dobrane są w ten sposób, że

(1.2)

0,320

-    płyty połączone są monolitycznie z belkami,' spełniającymi rolę podpór.

Przy równych rozpiętościach płyt lub gdy rozpiętości nie różnią się więcej niż H oraz gdy obciążenie rozłożone jest równomiernie, wówczas momenty zginające można określić według wzorów:

-    moment w przęśle skrajnym oraz moment krawędziowy na podporze przedslcrąjncj (środkowy w przypadku płyty dwuprzęsłowej)

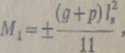
(U)

- momenty w przęsłach pośrednich oraz momenty krawędziowe na podporach pośrednich

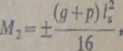
(1.4)

gdzie pip- rzeczywiste obciążenie stałe i zmienne, /, - rozpiętość w świetle żeber lub

wieńców; w przypadku płyt opartych swobodnie na murze do rozpiętości w świetle należy dodać 0,5 grubości płyty, a w przypadku nierównych przęseł moment podporowy oblicza

się przyjmując we wzorach większą z rozpiętości dwóch przyległych przęseł. - H Odstępy między żebrami zaleca się przyjmować według załączonej tab. 1.2, która została opracowana na podstawie zastosowania ekonomicznego procentu zbrojenia i możliwie minimalnej dopuszczalnej grubości płyty. Ekonomiczne rozpiętości przęseł płyty, które podaje tab. 1.2 można otrzymać następująco. Obliczamy maksymalny moment przęsłowy, na przykład dla skrajnego przęsła płyty wieloprzęslowej, który przy obciążę-liu sumarycznym wynosi:

dostępnie znajdujemy obliczeniową wysokość płyty, dla której przy szerokości fi= 1,0 m przyjmuje postać

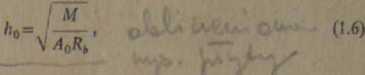
^v    (1.7)

gdzie k - współczynnik z tablic Winklera, A₀ - współczynnik z tablicy 7, zależny od próbni u zBrbjenia (patrz załączone "tablice na końcu podręcznika), rt_u, n_2l - współczynniki obciążenia wg PN-70/B-02009.

Tabela 1.2

Optymalne rozpiętości płyt

Grubość I	Całkowite obciążenie (»,,»+[kG/m^J]
płyty/i [cm]	300	300	ISO	1000	1300
UŁ	2,0-2.40	1,8 -2.4	1,6-2,4	. •» 5	_
7	2,1	2,4.0,8	2.0-2,8 <	1,7-2.0
8	-	2,8-3,0	2,2- 3,0	1.9-2,6	1.6-24

Przyrównując prawe strony równań (1.5) i (1.7) otrzymamy ekonomiczne rozpiętości

przęseł płyty    '

l=h₀

kfaug+Hnpy

(1.8)

gdzie h₀ w cm, g i p w kG/m^ł, / w m.

Ekonomiczne rozpiętości zarówno żeber, jak podciągów są równe około 6,0 m. W przypadku istnienia ścian działowych pod stropem żebrowym, należy żebra usytuować tak, by pokrywały się z osiami ścian. Elementy wieloprzęslowe stropu żebrowego o rozpię-tościach równych lub zmieniających się w granicach do 20% można przy regularnych obciążeniach (np. obciążenie ciągłe, siły skupione regularnie rozłożone) obliczyć za pomocą tablic Winklera. Wtedy dla momentów przęsłowych przyjmuje się rozpiętości rzeczywiste przęseł, dla momentów podporowych średnią arytmetyczną rozpiętości przęseł sąsiednich. Przy nieregularnym układzie przęseł i sił obliczenia przeprowadza się najlepiej za pomocą równań Clapeyrona lub metodą Crossa.

\

Oddziaływanie płyt i belek ciągłych na podciągi i słupy oblicza się zakładając rozdęcia i swobodne podparcia na podporach, tj. bez uwzględnienia ciągłości z wyjątkiem nacisku na środkową podporę elementów dwuprzęsłowych, przy którym oddziaływanie należy przyjąć o 20% większe, niż dla przęseł rozciętych, jeżeli wpływu częściowego utwierdzenia elementu na podporach skrajnych nie wykazuje się w obliczeniu, y

Przy obliczaniu naprężeń ścinających (głównych) w belkach ciągłych należy przyjmować siły poprzeczne i uwzględnieniem wpływu momentów podporowych.

Wysokości podciągów i rozpór ram o przekroju prostokątnym lub teowyra nie powinny być mniejsze od 1/15 rozpiętości przęsła w świetle, wysokości zaś żeber nic mniejsze niż 1/20 rozpiętości przęsła w świetle. Szerokość przekroju poddągów i żeber ustala się w zależ-