84722 P1010746 (3)

I

I

I

I

a ugięcie jej w środku rozpiętości wyn iesieji,, to w belce równoległej położonej w o<Ueg)₀

W belkach sąsiednich wystąpią momenty mniejsze. Wyliczamy je z proporcji ugu£ Jeśli w Belce środkowej biegnącej wzdłuż boku /, wystąpi moment zginający

<a' x o ugięciu w środku rozpiętości, np. f₂, moment zginający wyniesie

Rys. i. 108. Wykresy ugięć belek w stropie kasetonowym

(1-62)

Jm

Ponieważ przy założeniu jednostajnego obciążenia belek ugięcie dla kierunku /,w_p,, będzie miało wartość

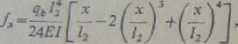
w środku zaś przęsła

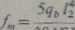
384El

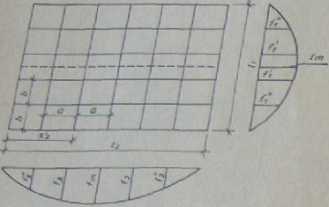
zatem wartość szukanego momentu zginającego M_lx dla kierunku I, wyniesie

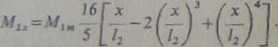
(1.64)

Odpowiednio dla kierunku /₂ będzie

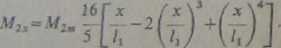
(1-65)

Obliczanie stropu kasetonowego wyżej omówioną metodą daje dość dokładne wyniki dla celów praktycznych. Pewna nadwyżka momentów zginających, dochodząca zależnie od rozstawu belek do 20% w stosunku do metod ścisłych, zwiększa stopień bezpieczeństwa konstrukcji, co niejednokrotnie pokrywa się z niedoborem wymaganej pewności, wynikłej z niedociągnięć wykonawstwa Jub warunków eksploatacyjnych stropu.

^nomnicć^^Jje^ji^icrws»j metody liczony był strop kasetonowy nad

^J^ych u* 1,58 m, rozstawy belek podyktowane były względami architektomcz-r^Crub⁰*¹' plyfy ze względów statycznych wystarczała 8 cm, przyjęto z powodu mniej-

ii)¹¹"' ^jcttia belek grubość płyty 12 cm. Szerokość belek dla obu kierunków wynosi 4* wysokość całkowita belek 70 cm, to jest około 1/20 mniejszej rozpiętości obbeze-belek. Obliczenie przekrojów zostało przeprowadzone metodą klasyczną; zbroje* ^Iki środkowej krótszej wynosi 10 0 25, zaś zbrojenie belki dłuższej 5 0 22, wkładki _l3j^owe górą w obu przypadkach 2015, strzemiona 010 co 25 cm.

•p^ obliczaniu belek w stropach kasetonowych dla rzutu kwadratowego można

^._5Wć z gotowych współczynników określających wielkość obciążenia poszczegól-j^lek oraz wartości momentów zginających, które podano w tab. 47.

Płytę stropu kasetonowego liczy się jedną z metod obliczania płyt krzyżowo zbrojo-

_th, omówionych w p. 1.3.1.

Strop kasetonowy posiada duże zalety natury konstrukcyjnej i ekonomicznej oraz

pj^wia ciekawy efekt architektoniczny, zatem w praktyce powinien znaleźć szersze glosowanie.

Przykład 10. Obliczyć strop kasetonowy nad salą o wymiarach w świetle murów /,=8,0 m, h = *li» »!> obciążenie użytkowe stropu p*=300 kG/m^J.

Przyjcto: grubość płyty tf'=8 cm, rozstaw belek a=i=U m. Wymiary belek: i=20 cm. A=45 cm, WwlUsy BI50 o *=85 kG/cm*, *_a=7,5 kG/cra^ł stal A-O StOS o *=*,=1900 kG/cm*. Obciążenia obliczeniowe (z uwzględnieniem współczynników obciążeń):

1) ciężar własny płyty    0,08-2400 1,1 =211 kG/m^J

2) ciężar podłogi z klepki dębowej    (0.022-750+2) 1,3= 25 kG/m^J

J) ciężar jastrychu    0,02-1100-1,3 = 36 kG/m^ł

41 ciężar tynku cem.-wap.    0,015-1900-1.3 « 38 kG/m^ł

5) ciężar użytkowy

razem

9=310 kG/m^ł 300-1.4=9=420 kG/m^ł q^m kG/m¹

P». I. Płyta

Płytę oblicza się jedną z metod podanych w p. 1.3, przy czym ze względu na niewielkie rozpiętości I [lii zbrojenie w nich wypada zwykle minimalne.

Obliczenie belek:

łi = 8,0-1,05 = 8.40 m, /, = 10,50-1,05=11,00 | łi=8,40⁺=4Q80 m⁴,    /,*» \ l,00^ł= 14600 m⁴;

15 wroni (1.59)

14600

14600+4080

■571 kG/m*.

4080

4080 +14600

= 160 kG/m¹.