Image0166

Natomiast przy założeniu c=45min optymalne wykorzystanie linii metra uzyskamy dla:

a = 1000 m - 1 km b = 2000 m = 2 km d = 6000 m = 6 km

Rezultaty wskazują, że prawidłowy dla mieszkańca miasta układ daje założenie c=30min mimo, że a jest w tym przypadku niewielkie rzędu 300m.

Układ ten ma jednak dwie wady:

1)    zbyt krótkie odstępy między przystankami metra ok.óOOm

2)    konieczność dwukrotnego przesiadania się przy maksymalnej podróży Natomiast wielką zaletą jego jest to, że maksymalna podróż nie trwa

dłużej niż 30min w mieście liczącym ponad 600tys. mieszkańców i nie traci się czasu na oczekiwanie na pojazd.

Typ 14

Ten typ jednostki miejskiej otrzymamy stosując układ pasmowo-obwodowy i dwa środki komunikacji zbiorowej o różnych prędkościach, np. autobus i metro, traktując autobus jako środek dowożący do metra, a metro jako główną rozrządową linię komunikacji zbiorowej.

Z wyliczeń otrzymaliśmy następujące wyniki:

dla czasu podróży równego 30min

a	b	d	P	M	pas	pas/l-kier
0.3	' 3.2	7.6	5764	1.152.800	125.425	62.712
0.45	2.3	6.4	4096	819.200	89.129	44.564
0.8	0,2	3,6	1.440	288.000	31.334	15.667

dla czasu podróży równego 45min

a	b	d	P	M	pas	pas/l-kier
0.3	5.7	12.6	15.876	3.175.200	345.462	172.730
0.45	4.8	11.4	12.996	2.599.200	282.780	141.400
0.6	3.9	10.2	10.404	2.080.800	226.390	113.200
0.7	3.3	9.4	8.836	1.767.200	192.270	96.150
0.75	3	9	8.100	1.620.000	176.260	88.150
0.78	2.82	8.76	7.674	1.534.000	166.980	83.500
0.8	2.7	8.6	7.396	1.479.200	160.940	80.500

Widoczne jest, że najkorzystniejszy układ dla pasażerów uzyskamy przy c=30min, a=0.45km, tj. dla jednostki miejskiej liczącej ponad 800 tys. mieszkańców, układzie pasmowo-obwodowym, obsłużonym przez jedną linię metra i pomocnicze linie autobusowe.

ck'-la{fl + y ~ 2)

h

2(r-i)

2(k'-k)

^ _ k'{yk'+x)

a a

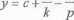
x =

lak

P

- lek - la

Wyniki analizy obrazują wykresy zależności powierzchni zabudowy

miasta P w [km^z] obsługiwanej przez dwa środki komunikacji oraz wielkości b

i doi

długości dojścia pieszego a.

Z danych przykładów i wykresów można wysnuć następujące wnioski:

1.    Powyższe wykresy są ważne dla jednoszynowej kolei w założeniu, że będzie ona przewozić tą samą liczbę pasażerów co metro.

2.    Z rysunku wynika, że przy c=30min, linia metra będzie wykorzystana maksymalnie, a powierzchnia obsłużonego terenu będzie największa dla a=600rn.

3.    Przykład z rys. 29 został wykonany dla a=1.000m.

4.    Z rys. 24 wynika, że przy c=45min, jedna linia metra będzie wykorzystana maksymalnie, a powierzchnia obsłużonego terenu będzie największa dla a—750m.

5.    Przykład (rys. 30) został wykonany dla a=1.000m.

6.    Z wykresu obrazującego zastosowanie jednoszynowej kolei miejskiej (rys. 25 i 26) widzimy, że dla przyjętych danych tj. prędkość komunikacyjna - ponad łOOkm/h, pojemność przewozowa identyczna jak w przypadku metra, maksymalne wykorzystanie tego środka komunikacji nastąpi dla a równego około l.OOOm, przy przyjętym czasię podróży równym 30min. Czyli dla takiego a- wartości dojścia pieszego - powierzchnia pod zabudowę miasta będzie największa.

Przy czasie podróży rzędu 45 minut jednoszynowa kolej nadziemna będzie przeciążona.