Image66 (7)

130

1

N =

Pr

T

CL.

Zatem całkowity moment sił, działający na rozważaną bryłę sztywną, wynosi

M = -3 Nr = -

Pr

T

CL,

a równanie ruchu bryły przyjmuje postać

0,

Pr²

^{a +} ir«

gdzie I jest momentem bezwładności bryły względem osi przechodzącej przez jej środek. Stąd

co

2 n

~T

Pr

U

a

I =

PT²r²

4n²l

Moment bezwładności tarczy

2J2

h =

PTjr 4n²l

moment bezwładności tarczy wraz z prętem

2_2

/

(P + Q) T\r 4n²l

a moment bezwładności pręta

h

r² [Tl (P + Q) - T^P]

4 n²l

2.89. Korzystając z zasady zachowania energii

d

dt

(E_k + E„)

0,

znajdujemy równanie ruchu walca

<P +

3 (R

a)

sincp — 0.

Dla małych wychyleń z położenia równowagi

sin (p

i równanie to przechodzi w równanie oscylatora harmonicznego

(p -|- a) (p

2_

0,

gdzie

Cl)² =

3 (R - a)

2.90. Na kulę poruszającą się po równi pochyłej bez poślizgu działają następujące siły (rys.48): siła ciężkości mg, reakcja R równi pochyłej, prostopadła do równi oraz tarcie T występujące na styku kuli z równią. Ruch ten możemy rozpatrywać jako ruch postępowy środka masy i ruch obrotowy dookoła osi przechodzącej przez środek masy. Mamy więc następujące równania ruchu:

mx

mg sina

T,

my = mg cosa

R,

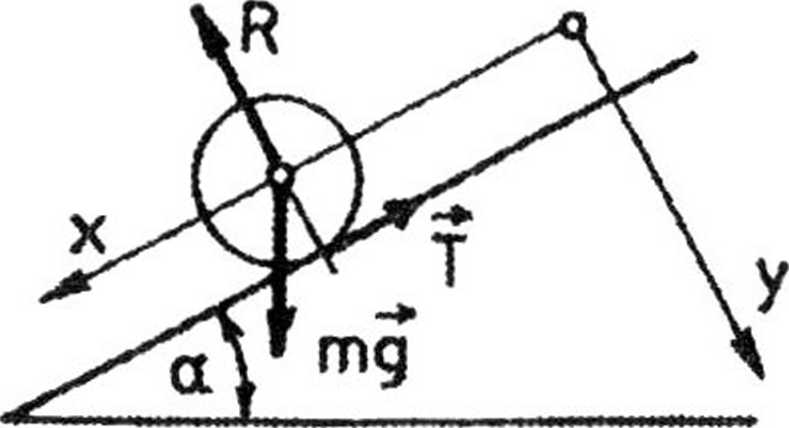
Rys.48

9 9

h<P

rT

Uwzględniając, że w każdej chwili