Image6 (49)

66 _Rozwiązania zadań ze zbioru "MENDLA"_

Za pi i P2 oraz objętość podstawiamy odpowiednie wyrażenia, Stąd (pa - p • b • a) • I • S = pa • I2 • S /: pa ■ S (pA - p • b • a) • I • S ^2_ p_A • S 11 _ I' (Pa ~ ^p' b' a)

PA

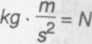
0,3m- (104000Pa- 13600-^ • 0,25m- 3-^)

■__rrr_s_

^2_    104000Pa

I2 = I2 =

0,3m • (104000Pa - 10200-—) _rrr

104000Pa 0,3m • 93800Pa

ale

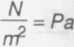
104000 Pa I2 = 0,27m = 27 cm

Odp.: Po zatrzymaniu się rurki długości słupka powietrza wynosi 27 cm.

Zadanie 582 str.116

Dane:    Szukane:

V1 = 100 cm³ = 0,1 dm^2,    P2 = ?

V2 = 10 drri³ N = 15

pi = 1100 hPa

Początkowo mamy pojemnik o objętości V2 wypełniony powietrzem o ciśnieniu atmosferycznym pa. Następnie dodatkowo wtłaczamy do tego pojemnika powietrze w ilości N = 15 pompek o objętości Vi.

Po dopompowaniu objętość powietrza wynosiła:

Vi' = V₂ + N • Vi

Objętość końcowa Mź = V2.

Ciśnienie początkowe wynosi pi , końcowa P2.

Z treści wiemy, że powietrze poddano przemianie izotermicznej, a więc

pi • Vi' = p2 • V2' , ale M2' = V2 oraz Vi' = V2 + N-Vi

stąd

Pi P2 = P1

(V2 + N • Vi) = P2 (V₂ + N- Vi)

V₂

/: V₂

V₂

P2 = P1

Vi

(¹ + N • vj)

p₂ = 11 OOhPa • (1 + 15 . Q'^1cfrTf)

10 drrP

p₂ = 1100/7Pa-(1 + 0,15)= 1100-1,15/?Pa= 1265hPa Odp.: W naczyniu panuje ciśnienie 1265 hPa.

Zadanie 583 str.117

Dane:    Szukane:

pi = 768 mmHg    p₄ = ?

P2 = 748 mmHg - temu ciśnieniu odpowiada

wysokość słupka rtęci h2 = 768 mm P3 = 734 mmHg - temu ciśnieniu odpowiada

wysokość słupka rtęci h3 = 734 mm

h « 8 cm = 80 mm

pi - ciśnienie atmosferyczne

p₄ - ciśnienie atmosferyczne przy wskazaniu barometru p3 = 734 mmHg

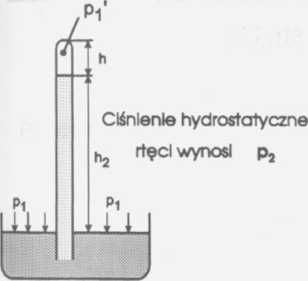
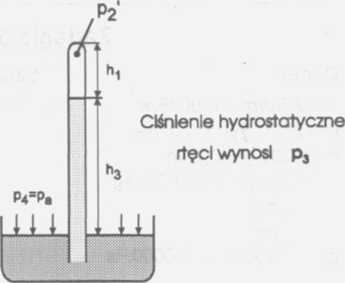
Barometr znajduje się w stałej temperaturze, więc z prawa przemiany izotermi-cznej dla gazu znajdującego się nad rtęcią otrzymamy:

Pi' • Vi = P2' • V2,	ale	P1 =P1' + P2
	stąd	pi' = pi - P2
	oraz	p4 = P2' + P3
		co CL I CL II k

Teraz wyznaczamy Vi i V2-Niech S będzie przekrojem rurki, więc:

Vi = S • h oraz V2 = S • hi Na podstawie rysunków mamy zależności: h + h2 = hi + h3 stąd hi = h + h2 + h3