Image42 (19)

171 Rozwiązania zadań ze zbioru "MENDLA”

Za pi • Vi do pracy W podstawimy n R • Ti.

stąd W = n • R • Ti • (k - 1)    /: [n - R - (k — 1)]

Ti =

Po przekształceniu otrzymamy szukaną temperaturę Ti. W

n • R • (k - 1)

Odp.: Temperatura początkowa i końcowa przemiany ma wartość okre-

W

śloną wzorem T, = _nR(k_₁₎.

Zadanie 678 str.134

Dane:

n = 1 W

Ta = Ti = T

Szukane:

k = — = ?

P2

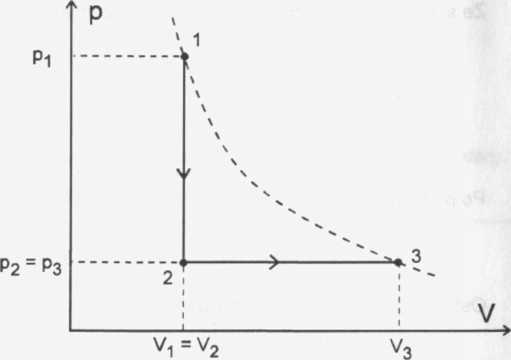
Aby wyznaczyć stosunek ciśnień k musimy skorzystać kolejno z praw rządzących wszystkimi przemianami gazu przedstawionymi na wykresie.

Podczas procesu 1-2 objętość gazu była stała, więc praca W = 0 , a cała praca W została wykonana przy przejściu gazu ze stanu 2 do 3.

Z wyrażenia na pracę mamy:

W = p • AV ,    ale    aV = \/z - M2

stąd W = p3 • (V3 - V2)

Przy przejściu ze stanu 2 do 3 ciśnienie było stałe (przemiana izobaryczna), więc:

/•t₂

skąd V2=

V2_ V3 T₂“T3 V3 • T2

Ta

Wyznaczone V₂ podstawiamy do wyrażenia na pracę.

W = p₃

N/3-T21

T3

i-f

T3

V3-

W = P3 • V3

W = p₃ • V₃

Ze stanu 1 do 2 gaz przeszedł w wyniku przemiany izochorycznej, więc:

Pl_ P2 Ti "T₂

Pi • T₂ = p2 • Ti

lecz

Pl = k

P2

/•P2

stąd pi = k • p2

Po podstawieniu za pi = k • p₂ mamy: k • P2 • T₂ = P2 ■ Ti /: k • p2

T₂ =

T2 =

P2 • Ti k • p₂

Ii k

Wyznaczoną temperaturę T₂ podstawiamy do pracy W.

W = p₃ • V₃

W =

P3 • V3

T₃

_T T,

^T3-Y

t₃

T ^T1

^T3"Y

P3 • Vą

W ostatnim równaniu nie znamy wartości wyrażenia ^    , więc musimy sko

rzystać z równania Clapeyrona dla stanu 3.

Eą-^Un.R

T3

Iloczyn n • R podstawiamy do wzoru na pracę,

skąd W = n-R-(T₃-y)

/: n • R

lecz

Ti = T₃ = T

więc

W _    T

n - R“    k

Teraz możemy przekształcić ostatnie wyrażenie i obliczyć k. W

k ^T n • R

/■k

n-R-T-W n • R

/:

•p n - R -T-W . n • R

k - T •--

n-RT-W