8.1 Twierdzenia dotyczące programowania nieliniowego

W programowaniu nieliniowym podstawowe znaczenie mają dwa rodzaje funkcji

1) wypukła (mówi się o programowaniu wypukłym)

2) wklęsła

Zadaniem programowania wypukłego nazywamy takie zadanie programowania nieliniowego, w którym:

- minimalizujemy wypukłą bądź maksymalizujemy wklęsłą funkcję celu

- zbiór rozwiązań dopuszczalnych jest zbiorem wypukłym

Zadaniem programowania wklęsłego nazywamy zadanie nie wypukłe, w którym:

- minimalizujemy wklęsłą bądź maksymalizujemy wypukłą funkcję celu

- zbiór rozwiązań dopuszczalnych jest nadal zbiorem wypukłym

Niektóre zadania programowania nieliniowego dają się sprowadzić do zadań liniowych, i takim typowym przykładem jest programowanie ilorazowe

8.2 Zagadnienie transportowe

Jako jedno z zagadnień programowania liniowego. Po raz 1 zostało sformułowane przez Hitchcok'a w 1941r.

Ekonomiczne zagadnienie transportowe można przedstawić w następujący sposób:

Danych jest m-dostawców (i) pewnego jednorodnego produktu. Zasoby tego produktu znajdujące się u i-tego dostawcy wynoszą a_i. Produkt jest przeznaczony dla n-odbiorców (j) których zapotrzebowanie wynosi odpowiednio (b_1,b₂…b_n). Koszt transportu jednostki tego produktu od i-tego do j-tego odbiorcy wynosi c_ij.

Należy określić plan przewozów pomiędzy dostawcami a odbiorcami, aby uwzględnić dostępne zasoby dostawców i wymagane zapotrzebowania odbiorców tak, aby łączne koszty transportu były minimalne.

X_ij - zmienna decyzyjna, określająca wielkość przewozu od i-tego dostawcy do j-tego odbiorcy

Przed przystąpieniem do matematycznej budowy modelu musimy określić, czy zagadnienie jest zbilansowanie czy niezbilansowane (zamknięte czy otwarte)

8.3. Opisać zagadnienie dualizmu (dualizm w programowaniu liniowym)

Charakteryzuje się tym, że każde zadanie programowania liniowego polegające na maksymalizacji (minimalizacji) posiada pewne ekwiwalentne zadanie programowania liniowego polegające na minimalizacji (maksymalizacji).

Przyjmuje się, że oryginalne sformułowanie problemu jest zadaniem prymalnym (pierwotnym) natomiast sformułowanie alternatywne jest zadaniem dualnym (wtórnym)

L(x)=C^TX max A^*X B X 0

L(y)=B^TY min A^TY C Y 0

8.4 Ograniczona pojemność magazynu (wielkość zapasów)

Przyjmujemy założenia od a do h modelu klasycznego:

1. zapotrzebowanie na rozpatrywany zasób przypadające na okres [0,T] jest znane i wynosi Q

2. zużycie zasobów jest równomierne w czasie

3. zakup zasobu w okresie [0,T] dokonywany jest n razy w jednakowych odstępach czasu t_o gdzie t_o=
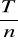
   , w partiach w jednakowej wielkości S=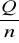
   

4. zamówienia składane są wyprzedzająco tak, aby dostawa kolejnej partii nastąpiła w momencie zużycia poprzedniej

5. zapotrzebowanie w każdym momencie okresu [0,T] musi być zaspokojone, tzn. nie dopuszczany jest niedobór zapasu.

6. W okresie [0,T] cena jednostkowa zasobu nie ulega zmianie

7. Koszt magazynowania jest wprost proporcjonalny do wielkości zapasu

8. Koszt realizacji zakupu nie zależy od wielkości partii i dla pojedynczej partii wynosi K.

Wprowadzamy dodatkowe założenie:

9. Pojemność magazynu jest ograniczona i nie może przekroczyć znanej wielkości B, tzn S
   B

Dlatego do funkcji celu modelu I należy dołączyć warunek ograniczający, wówczas:

D=c₁
+K
--> min przy warunku 0
S
B problem rozwiązujemy metodą mnożników Lagrange'a, w wyniku czego otrzymujemy:
wyznaczamy wartość optymalną pojedynczej partii zakupu.

---