Optymalny wybór asortymentu produkcji
Zakład może produkować n wyrobów. Do ich produkcji zużywane są różne środki produkcji, z których część (m) jest dostępna w ograniczonych ilościach. Dane są normy zużycia środków produkcji na jednostkę każdego wyrobu, dane są zasoby środków produkcji oraz ceny bądź zyski jednostkowe. Mogą być znane informacje dotyczące popytu produkowanego wyrobu oraz minimalne ilości wyrobów jakie trzeba wyprodukować (podaż). Które wyroby i w jakich ilościach produkować aby nie przekraczając posiadanych zasobów środków produkcji maksymalizować przychód (lub zysk) z ich sprzedaży
MODEL:
![]()
![]()
![]()
![]()
(j=1,2,…n)
![]()
- zużycie i-tego środka produkcji na wytworzenie jednostki j-tego wyrobu
![]()
- posiadany zasób i-tego środka produkcji
![]()
- cena lub zysk jednostkowy ze sprzedaży j-tego wyrobu
![]()
- minimalna ilość ilość-tego wyrobu jaką trzeba wyprodukować
![]()
- maksymalna ilość j-tego wyrobu jaką trzeba sprzedać (ograniczenie popytowe)
![]()
- wielkość produkcji j-tego wyrobu
1.2. Własności zadania transportowego
Twierdzenie I:
W każdym zbilansowanym zadaniu transportowym zbiór rozwiązań dopuszczalnych jest niepusty i ograniczony Wniosek: Każde zagadnienie transportowe posiada skończone rozwiązanie optymalne
Liniowe zadanie decyzyjne dotyczące zagadnienia transportowego w postaci kanonicznej można zapisać następująco:
K=CTX min
AX=B
X![]()
0
Gdzie:
x- wektor zmiennych decyzyjnych wymiaru (m-n)x1
C - wektor współczynników funkcji celu wumiaru (m-n)x1
A- macierz współczynników występujących w warunkach ograniczających wymiaru (m+n)x(m-n)
B- wektor wartości brzegowych warunków ograniczających wymiaru (m+n)x1
Twierdzenie II:
Rząd macierzy A warunków ograniczających zadania transportowego jest równy m+n-1
Wniosek: Zmiennych bazowych w rozwiązaniu zadania transportowego jest dokładnie m+n-1
Twierdzenie III:
Jeżeli wszystkie ai i bj (dla i=1,2…m, i j=1,2…n) są liczbami całkowitymi to każde rozwiązanie bazowe (również optymalne) jest utworzone z liczb całkowitych
1.3. Wieloetapowy proces decyzyjny i punkt siodłowy
Dolną wartością gry nazywamy liczbę v1=max min W(s,t)
Strategia odpowiadająca dolnej wartości gry v1 nosi nazwę strategii maxyminowej. Strategia maxyminowa jest najostrożniejszą strategią gracza P1 gwarantującą mu wygraną na poziomie co najmniej v1.
Górną wartością gry nazywamy liczbę v2=min max W(s,t)
Strategia odpowiadająca górnej wartości gry v2 nosi nazwę minimaxowej gacza P2. Minimaxowa strategia gracza P2 jest najostrożniejszą strategią gwarantującą graczowi drugiemu, że nie przegra więcej niż v2.
Jeżeli v1=v2 to mówi się, że gra posiada tzw. punkt siodłowy. Jeśli dla gry istnieje punkt siodłowy, to gra kończy się wówczas dla obu graczy. Strategie czyste odpowiadające temu punktowi nazywami strategiami optymalnymi.
Jeśli gra nie posiada punktu siodłowego, czyli v1 ![]()
v2 to strategie optymalne obu graczy są strategiami mieszanymi (nie czystymi).
1.4. Na czym polega problem gry z naturą, jak można zastosować kryterium optymalności
Gra z naturą - gra 2-osobowa o sumie zero, w której graczem P1 jest organ podejmujący decyzję, a graczem P2 natura. Natura jest graczem nie myślącym, któremu nie zależy na wyniku gry.
Strategię decydenta w grze z naturą noszą nazwę decyzji, a strategie natury nazywa się stanami natury. Wynikiem gry z naturą może być zarówno wygrana natury, jak i wygrana decydenta. Wynik ten określa się na ogół za pomocą funkcji straty lub za pomocą funkcji efektywności decyzji.
Kryterium:
Bayes'a - maksymalizacja oczekiwanego zysku (wybieramy największy zysk)
Walda (pesymistyczne) - maksymalizacja najmniejszych możliwych korzyści maksyminowe
Savage'a (minimalnego żalu) oceniamy skutki nietrafnej decyzji. Tworzy się macierz straconych szans, której elementy są potencjalnymi stratami
Hurwicza - wyznacza się średnią ważoną najgorszego i najlepszego rezultatu, kryterium zależy od postawy decydenta, jest bardzo subiektywne
Laplace'a (braku dostatecznej racji) - dla każdej decyzji liczy się średnią arytmetyczną, zakłada się równe prawdopodobieństwa dla wszystkich stanów natury, wybiera się tą decyzję, gdzie średni zysk jest najwyższy
1.5 Model planowania zapasów dopuszczający niedobór zapasów
Przyczyny niedoborów:
związane z mobilnością
w wyniku zakłóceń produkcyjnych (owe zakłócenia mogą powodować niedobór, pojawi się koszt braków - trzeba będzie dokupić wówczas po cenach wyższych oraz koszt utraconych możliwości powiększający koszt niedoboru)
Przyjmujemy założenia z modelu I (klasycznego):
zapotrzebowanie na rozpatrywany zasób przypadające na okres [0,T] jest znane i wynosi Q
zużycie zasobów jest równomierne w czasie
zakup zasobu w okresie [0,T] dokonywany jest n razy w jednakowych odstępach czasu to gdzie to=
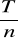
, w partiach w ojednakowej wielkości S=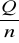
zamówienia składane są wyprzedzająco tak, aby dostawa kolejnej partii nastąpiła w momencie zużycia poprzedniej
W okresie [0,T] cena jednostkowa zasobu nie ulega zmianie
Koszt magazynowania jest wprost proporcjonalny do wielkości zapasu
Koszt realizacji zakupu nie zależy od wielkości partii i dla pojedynczej partii wynosi K.
Natomiast założenie e zmienia się na : dopuszczalny jest niedobór zapasu, przy czym jednostkowy koszt tego niedoboru C2 jest wprost proporcjonalny do wielkości niedoboru.
Średni zapas przez pierwsze t' jednostek każdego cyklu wynosi Z=![]()
przy czym udział czasu w przedziale [0,T] w ciągu którego zapas jest dodatni wynosi ![]()
.
Celem jest wyznaczenie S' i S w taki sposób aby łączne koszty magazynowania, realizacji, zakupu oraz niedoboru zapasu w okresie [0,T] były minimalne stąd ![]()
biorąc pod uwage, że ![]()
=![]()
mamy:
![]()
koszt realizacji zakupów ![]()
Następnie należy określić koszt niedoboru zapasu
Wynosi on 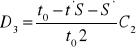
funkcja celu jest zatem następująca:
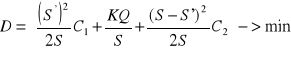
Funkcja osiąga minimum dla takich S i S', dla których:
![]()
; ![]()
z ostatniego wynika, że:
![]()
(*)
Z pochodnych oraz z tego, że ![]()
mamy: SS'=![]()
(**)
Ze wzorów (*) i (**) otrzymamy szukane optymalne S i S'
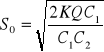
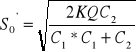
Wyszukiwarka
Podobne podstrony:
pytania egz, badania zestaw 3
pytania egz, badania zestaw 8
pytania egz, badania operacyjne - poza zestawami
pytania egz, BADANIA OPERACYJNE, BADANIA OPERACYJNE
pytania egz, BADANIA OPERA, BADANIA OPERACYJNE
pytania egz, BADANIA OPERACYJNE1-pytania, BADANIA OPERACYJNE
pytania egz, BADANIA OPERACYJNEee, BADANIA OPERACYJNE
pytania egz, BADANIA OPERACYJNE1-pytani, BADANIA OPERACYJNE
pytania egz, badania operacyjne - pyt, I
pytania egz, badania operacyjne2, I
pytania egz, ZESTAW 3, ZESTAW 3
pytania egz, ZESTAW 1, ZESTAW 1
pytania egz, ZESTAW 4, ZESTAW 4
pytania egz, ZESTAW 6, ZESTAW 6
Pyt.egz 4, Pytania egz zestaw 4
Mechanika Semest I pytania egz
PSYCHOPROFILAKTYKA PATOLOGII SPOŁECZNEJ pytania egz, Terapia
pytania egz ekonimak II, OPRACOWANIE PYTAŃ NA EGZAMIN
pytania egz.fizjot.-1, pedagogika, egzamin
więcej podobnych podstron