Ciała stałe można podzielić na : przewodniki, półprzewodniki i dielektryki (izolatory). Półprzewodniki są to ciała których konduktywność jest mniejsza od konduktywności dobrych przewodników, ale zarazem znacznie większa od konduktywności dielektryków (są to granice
). Podział ten jest bardzo przybliżony. Istotnym czynnikiem, który odróżnia półprzewodniki od pozostałych grup ciał stałych, jest ich struktura elektronowa.

W odosobnionym atomie, w normalnym niepobudzonym stanie, elektrony zajmują wszystkie najniższe poziomy energetyczne. Również w ciele stałym poziomy pasm najniższych są całkowicie obsadzone przez elektrony. W myśl tzw. zasady Pauliego każdy dozwolony poziom energii może być obsadzony przez najwyżej dwa elektrony. Aby przewodzić prąd elektryczny, elektron musi pobierać energię od przyłożonego pola elektrycznego. Oznacza to, że elektron musi być przenoszony na wyższe poziomy energetyczne, co w/g Pauliego jest niemożliwe, jeśli poziomy te są już zajęte (elektrony wewnętrzne). Dla przewodnictwa elektrycznego istotne jest wypełnienie pasm przez zewnętrzne elektrony walencyjne.

W przewodnikach (metalach) elektrony walencyjne tylko częściowo wypełniają pasmo, albo najwyższe całkowicie obsadzone przez elektrony walencyjne pasmo nachodzi częściowo na wyżej położone pasmo puste, dając w końcu też pasmo częściowo zapełnione. Elektrony walencyjne mogą przechodzić na wyższe, nie zajęte poziomy. Zatem w obecności zewnętrznego pola elektrycznego, elektrony najwyższego częściowo zapełnionego pasma (pasma przewodnictwa) mogą pobierać od pola energię, tworząc uporządkowany ruch ładunków, czyli prąd.

W dielektrykach elektrony walencyjne całkowicie wypełniają pasmo walencyjne (podstawowe). Wyżej leżące pasmo przewodnictwa jest oddzielone od pasma walencyjnego szerokim pasmem energii wzbronionej. Elektrony walencyjne w tym przypadku nie mogą pobierać od zewnętrznego pola elektrycznego, gdyż z.Pauliego nie pozwala im przechodzić na wyższe, zajęte poziomy pasma podstawowego. Przejście elektronów walencyjnych do pustego pasma przewodnictwa jest praktycznie niemożliwe. Prąd w dielektrykach w zasadzie nie płynie.

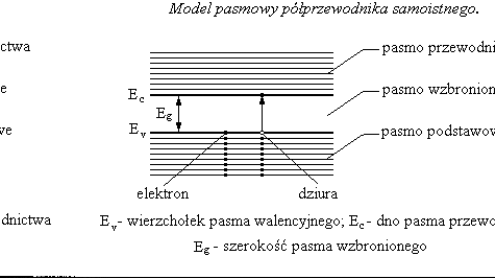
W półprzewodniku część elektronów pasma walencyjnego może przejść do pustego pasma przewodnictwa i stać się elektronami zdolnymi do przewodzenia prądu. Wcześniej należy jednak elektronom walencyjnym dostarczyć energii równej szerokości pasma wzbronionego. Energia ta może być np. energią drgań cieplnych siatki krystalicznej, proporcjonalną do temperatury ciała.

Dzięki małej szerokości pasma wzbronionego w półprzewodniku, już w temperaturze pokojowej część elektronów walencyjnych jest przeniesiona do pasma przewodnictwa i umożliwia przepływ prądu ( w dielektryku w temperaturze pokojowej pasmo przewodnictwa jest całkowicie puste).

W metalach swobodnymi nośnikami ładunku są elektrony niezapełnionego pasma przewodnictwa i konduktywność wyraża się wzorem

σ=enu_n

Koncentracja swobodnych nośników n w metalach w odróżnieniu półprzewodników nie zależy od temperatury i jest rzędu koncentracji atomów.Koncentracja swobodnych nośników w metalach jest o kilka rzędów większa niż w półrzewdnikach.Ruchliwość swobodnych nośników ładunku

u_n=v_n/E ustala się w warunkach równowagi, gdy średni przyrost prędkości unoszenia v_n ,wywołany działaniem siły pola elektrycznego E jest równoważony ubytkiem tej prędkości, wywołanym procesami rozproszeniowymi.

W metalach można rozróżnić dwa podstawowe mechanizmy rozpraszania.

W zakresie wysokich temperatur decydujące jest rozpraszani swobodnych nośników, związane z drganiami cieplnymi atomów, rozmieszczonych w węzłach periodycznej sieci krystalicznej. Dragania powodują niejednorodność ośrodka w postaci lokalnych fluktuacji gęstości, na których rozprasza się fala, reprezebtijąca ukierunkowaną w polu elektrycznym wiązke elektronów. Ponieważ energia drgań sieci jest skwantowana i kwant energii takich drgań o częstotliwości v wynosi hv i nazywa się fononem, można powiedzieć, że rozpraszanie swobodnych elektronów, spowodowane drganiami sieci, polega na zderzeniach elektronów sieci, polega na zderzeniach elektronów z fononami. że wzrostem temoeratury zwieksza się zarówno amplituda drgań sieci, jak i przekrój czynny na rozprasznie. Ze wzrostem temperatury maleje zatem ruchliwoąć i konduktancja metali; zwiększa się więc ich rezystancja.W zakresie wysokich temperatur, w mało zanieczyszczonych metalach jednoskładnikowych, z dobrym przybliżeniem słuszna jest liniowa zależność między przyrostem rezystancji metali a przyrostem temperatury.

Zależność tą opisuje wzór:

R_t=R₀(1+α₀t) gdzie:

R₀-rezystancja w temperaturze 0⁰C

R_t-rezystancja w temoeraturze t ⁰C

natomiast

α₀=(R_t-R₀)/R₀t nazywamy współczynnikiem temperaturowym rezystancji w zakresie od 0 do t ⁰C

Drugim mechanizmem rozprasznia swobodnych nośników w metalach jest rozpraszanie na wszelkich defektach sieciowych (zaburzenia strukturalne sieci).

W czystych metalach jednoskładnikowych ten typ rozprasznia ma dominujące znaczenie w bardzo niskich temperaturach. Wówczas składowa rezystancji R_i, spowodowana defektami sieciowymi, jest praktycznie niezależna od temperatury i mała w porównaniu ze składową rezystancji R_l, spowodowaną drganiami sieci w temperaturze pokojowej.

Rezystancja niektórych materiałów gwałtownie spada do zera po osiągnięciu pewnej dostatecznie niskiej temperatury, zwanej krytyczną. Materiały takie nazywamy nadprzewodnikami.

Dla półprzewodnika, wzakresie temperatur przewodnictwa samoistnego, mierząc zależność rezystancji od temperatury, można wyznaczyć szerokość pasma wzbronionego E_g (przerwę energetyczną).Korzystamy ze wzoru:

R=R₀exp(E_g/2kt)

gdzie R z dobrym przybliżeniem jest stałą zależną od rodzaju półprzewodnika i jego wymiarów geometrycznych

Część pomiarowa:

Schemat połączeń:

Przyrządy użyte w ćwiczeniu:

- Komora pomiarowa zawierająca badany metal (Pt) i stop półprzewodnikowy NTC 21;

- Multimetr typu 1321 szt.2;

- Autotransformator typu AR 201;

- Transformator ochronny.

Pomiar rezystancji w temperaturze pokojowej 24C :

półprzewodnik - 10,36 k

metal - 0,1075 k

Podwyższając stopniowo napięcie zasilania grzejnika za pomocą autotransformatora[a], powoli podwyższano temperaturę w sposób przedstawiony w tabeli. Pomiar wykonywano co 5C.

WZROST TEMPERATURY

temp.		R.met		1000/temp		Rpółprzew
296,15		0,109		3,37		10,92
298,15		0,111		3,35		9,49
303,15		0,113		3,30		7,60
308,15		0,115		3,25		6,09
313,15		0,117		3,19		4,90
318,15		0,119		3,14		4,01
323,15		0,121		3,09		3,28
328,15		0,123		3,05		2,73
333,15		0,125		3,00		2,19
338,15		0,128		2,96		1,84
343,15		0,130		2,91		1,51
348,15		0,132		2,87		1,27
353,15		0,134		2,83		1,05
358,15		0,136		2,79		0,90
363,15		0,138		2,75		0,74

Po wyłączeniu autotransformatora, włączono wentylator w komorze pomiarowej. A od temp 50C włączono dodatkowo chłodzenie wodne.

SPADEK TEMPERATURY

temp.	R.met	1000/temp	R.półprz
298,15	0,109	3,35	11,53
303,15	0,111	3,30	9,33
308,15	0,112	3,25	7,78
313,15	0,114	3,19	6,52
318,15	0,116	3,14	5,43
323,15	0,118	3,09	4,51
328,15	0,120	3,05	3,69
333,15	0,123	3,00	2,88
338,15	0,125	2,96	2,27
343,15	0,128	2,91	1,62
348,15	0,130	2,87	1,36
353,15	0,132	2,83	1,14
358,15	0,135	2,79	0,96

WYKRESY ZROBIONE SA DLA WZROSTU TEMPERATURY

1. Dokładność multimetromierza:

+/- (0,2 % wartości mierzonej + 0,1% podzakresu)

************	zakres
metal	2 k
polprzewodnik	20 k

2. Współczynnik temperaturowy ( )obliczamy ze wzoru:

α=(R_t-R₂₃)/R₂₃(t-23⁰)

α_m=0,00397

3. Szerokość przerwy energetycznej obliczamy ze wzoru :

tgφ=10^-3E_g/2k

E_g=(2k/10^-3)^.tgφ=2^.10^3.k^.(lnR₂-lnR₁)/(1000/T₂-1000/T₁ )

- gdzie ln R1, 1000/T1 oraz ln R2, 1000/T2 oznaczają współrzędne punktów na początku i końcu prostoliniowego odcinka wykresu zależności ln R = f(1000/T).

- odczyt kąta z wykresu : = 53 tg =1,32

E_g=2^.1,38^. 1,32 ^.10³/10²³=3,662^.10^-20JK

WNIOSKI:

Patrząc na wykres zalezności rezystancji od temperatury widać charakter liniowy wspomnianej właściwości co jest potwierdzeniem często wykorzystywanego wzoru (dla metali) R_t=R₀(1+α₀t);

Współczynnik przewodnictwa cieplnego α określa tangens nachylenia krzywej względem osi ox.

Podobnie sytuacja przedstawia się w przypadku drugiego wykresu. Kąt nachylenia krzywej umożliwia pomiar (w zakresie przewodnictwa samoistnego) szerokości pasma wzbronionego E.

Każdy wykres i uzyskane wartości są obarczone pewnym błędem który wynika generalnie z wielu powodów. Błędy pomiarowe które są bardzo trudne do wyeliminowania, gdyż wynikają z nidokładności i niedoskonałości urządzeń pomiarowych:

-miernika rezystancji

-termometru (błąd paralaksy przy odczycie określonej wartości)

- wpływ rezystancji użytych połączeń i przewodów

-opóżnienie odczytu rezystancji względem odczytu temperatury(ma duże znaczenie prz szybkim schładzaniu )

-błędy wynikające z zakłóceń zewnętrznych (drgania, niestabilność zasilania multimetrów),

Wszystkie w/w przyczyny składające się na ogólny wynik możnaby w lepszych warunkach w znacznym stopniu wyeliminować.

-------------------------------UZUPELNIENIE---------------------------------------------

Jak już wcześniej było wspomniane wykresy zawarte w tym sprawozdaniu zawierają wartości dla wzrostu temperatury, co w cale nie oznacza że dla spadku temperatury wykresy nie byłyby zgodne z oczekiwaniami. Ich brak wynika

jedynie z przyczyny czysto technicznej.

SPRAWOZDANIE

Z CW.NR 44

BADANIE ZALEZNOSCI REZYSTANCJI

OD TEMPERATURY DLA

METALI I POLPRZEWODNIKOW

---