044 045

i

i

2

Rozdział

SYNTEZA UKŁADÓW KOMBINACYJNYCH

Układy kombinacyjna opisywane są tabelą lub zaspołam funkcji logicznych wiążących każde wyjście układu z wejściami. Wyznaczenia jednego z tych opisów na podstawie zadanego słownego opisu działania układu nazywa się, jak pamiętamy! syntezą abstrakcyjną.

Przykład 2.1

Podać opis układu kombinacyjnego mnożącego dwie dwubltowe liczby binarne.

Układ posiada 4 wejścia (2x2)14 wyjścia, gdyż największy wynik mnożenia dwu liczb dwubltowych wynosi:

(11)₂ x (11)₂ * (1001)₂ * (9)ąo

Oznaczając wejścia przez i-jkg ¹ ^1*2 ^oraz wyjścia przez ^zi«^z2’^z3'^z4 otrzymujemy tabelę Jak na rys. 2.1.

Jak widać, układ opisany Jest przez 4 funkcje logiczne z^,z₂,zj.z^.Funkcje te zapisane w ZNPS 1 NP$ mają postać

*1 = ^x1^r2^y1^y2

z₂ = x₁I₂y₁y₂ + x₁x₂y₁y₂ + x₁x₂y₁y₂ = x₁x₂y₁ ♦ x^7_z

*3 “ ^x1^x2^y1^y2 ⁺ x1^x2^y1^y2 ⁺ X1^X2⁷1⁷2 ⁺ x1^2^y1^y2 ⁺ x1^x2^y1^y2⁺

+ *-l^x2⁷1^y2 “ ^X1^X2?1 + ^x2^y1^y2 ^{+ x}1^y1^y2 ^{+ x}1^x2^y2

^z4 ^{3 x}1^x2^y1^y2 ^{+ x}1^x2^y1^y2 ^{+ x}1^x2^y1^y2 ^{+ x}1^x2^y1^y2 ^{= x}2^y2 .

Układy kombinacyjne buduje się z elementarnych układów opisywanych prostymi funkcjami logicznymi. Te elementarne układy nazywają się funktorani lub bramkami logicznymi. Następny etap syntezy, zwany syntezą strukturalną, polega na otrzymaniu układu o zadanym opisie poprzez odpowiednie połączenie możliwie małej Ilości funktorów**. Okazuje się (patrz p. 2.2),że schemat połączeń wynika bezpośrednio z wyraźenla definiującego funkcję lo-

lane setody syntezy strukturalnej, z wykorzystanies multiplekserów t pastęel stałych BOM 1 PLA, eadwlone będą w rozdziale 4.

glczną opisujprojektowań; układ. .Pojawia się więc Istotny problem zapisywania funkcji logicznych w możliwie prostej postaci, zwany minimalizacją.

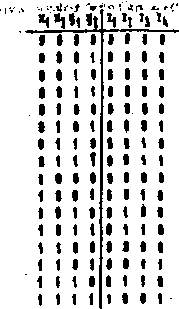
Rys.

2.1. MINIMALIZACJA FtJNKCJI LOGICZNYCH

Z problemem upraszczania wyrażeń logicznych spotkaliśmy się już w p. 1.3.1 (przykład 1.19). Tutaj usystematyzujemy to zagadnienie 1 podamy dwie podstawowe algorytmiezhe metody minimalizacji.

2.1. Tablica układu mnożąoego liczby dwu-bltowe

Omówimy metody upraszczania zapisów funkcji w przypadku, gdy postacią początkową jest ZNPS lub ZNPI, a postaciami końcowymi zapisy UPS i NPI o możliwie małej liczbie możliwie prostych. składników.

reguł sklejania.

(2.1)

(2.2)

Minimalizacja funkcji logicznych polega na wielokrotnym stosowaniu do upraszczanej funkcji tzw.

\ Ax + Ax (A + x)(A + X)

Wyrażenia podlegające sklejaniu noszą nazwę sąsiednich. Są one iloczynami lub sumami tych samych zmiennych różniącymi się tylko negacją jednej zmiennej. Np. sąsiednimi są wyrażenia x^x₂x^ 1 x^x₂x^ oraz x₁+x₂+ +5^+5^ i x₁+x₂+Xj+Xąt ich suma i iloczyn po zastosowaniu reguł sklejania wynoszą odpowiednio x^x₂ oraz x₁+i₂+x₃

Stosując wielokrotnie¹⁵ reguły sklejania do wyjściowych ZNPS można uzyskać postać minimalną, jednakże proces ten należy przeprowadzać umiejętnie, aby nie doprowadzić do sytuacji, w którsj dalszs sklejanie nie jest już możliwe, a nie otrzymano jeszcze postaci minimalnej.

Przykład 2.2

Zminimalizować funkcję

y = x^x₂x^ + x₁x₂x^ + x₁x₂Xj + x^x₂x^ + x₁x₂Xj

Nie wystarczy tu np. skleić składniki 213 oraz 5 i 7, bo otrzymamy wtedy

y = x₁x₂ + x₁x₃ + x₁i₂x₃

do ktćrej to postaci nie da się już zastosować reguły sklejania, a jak za chwilę zobaczymy nie jest to postać minimalna.

1

⁵ Przy .sklejaniu pamiętany o tożsamoiciach x = x+xe...+x oraz x = x-x ... x, pokazujących, ta pojedynczy składnik można sklejać z wie łona innymi.