140 141

140

O

Przy syr.tazle układów kombinacyjnych z użyciem multiplekserów, w za lenno śel od wyboru argumentów podawanych na wejścia adresowa multipleksera, układy realizujące funkcje pozostałych argumentów mogą olei ró«aą złoio* nośd - powstaje więc problem optymalizacji wyboru tych argumentów,

£%BijflaŁJŁz2.

Korzystając z branek 1 multipleksera o 2 wejściach adresowych zrsaii-zowąd układ opisany funkcją

f(x₁,x₂,x_?,z₄) = 2(0,2,3,5,7,11,12,14)

Zapisując funkcję w postaci ZNPS mamy f(x₁,x₂,-i₃,-:_ił) *    ♦ 5₁5₂x₅S_!,. •> ⁵t^S2^x3^xa + wyżytą t

+ i₁x₂w₃x_ł ♦ ^*3X5*4 t *1²2%^X4 ⁺ *1*2*1*$

Przyjmijmy, że na wejścia adresowe multipleksera podamy argumenty x₃ 1 *_Jł. Wyłączając przed nawiasy z realizowanej funkcji wszystkie Iloczyny argumentów Xj 1 oraz minimalizując wyrażenia w nawiasach ct .zyiui.jeay

( 'i ‘^2'"^3'^‘4) ⁼    (^■'1^2 ^ S-j~₂) ¹    Uf (^x2'

•*■ XjX₄(x₁x₂ + x.,x₂) + x₃x₄(x₁ + jćg)

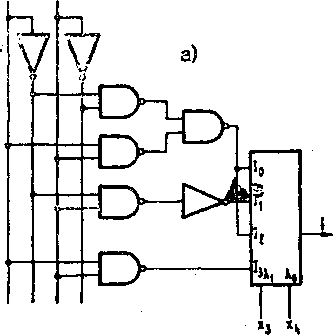
Schemat poszukiwanego układu przedstawiono na rys, 5»13a-

b)

»}

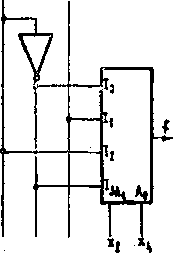
tiplekaera o 2 wejściach adresowych: a) schemat gdy na wejścia adresowe podano argumenty x. 1 i-, b) schemat gdy na wejścia adresowe podano argumen-^{} ą}    ty x, 1 1,

Podając na wejścia adresowe zmienne x₂ i x₄ otrzymujemy

f(x₁,x₂,x₃,x₄) =    + i₂x₄(x₃) + x₂x₄(x₁) + x₂x₄(x₁)

a wynikający schemat przedstawiono na rys. 5«13b.

Z otrzymanych wzorów lub ze schematu widać, że realizacja funkcji w przypadku podania na wejścia adresowe multipleksera zmiennych x₂ i x₄ jest znacznie prostsza. Czytelnikowi pozostawiamy sprawdzenie schematów w pozostałych przypadkach.    tż

Widać więc, że wybór zmiennych podawanych na wejścia adresowe jest bardzo istotny. Nie podajemy tu jednak żadnej metody poszukiwania optymalnego wyboru poza przejrzeniem 'wszystkich możliwych wyborów, których jest oczywiście (^) gdzie n jest ilością zmiennych, a m ilością wejść, adresowych multipleksera.

Reasumując stwierdzamy, że stosowanie multiplekserów do syntezy układów kombinacyjnych Jest wygodnym środkiem zmniejszającym na ogół ilość układów scalonych i upraszczającym' projektowanie.

5.3. DEMUI/TIPLEKŚERY

Demultiplekser jest układem działającym odwrotnie do multipleksera.Posiada on Jedno wejście informacyjne, N wejść adresowych oraz 2^N wyjść. Podanie adresu powoduje połączenie wejścia z wybranym przez adres wyjściea

o-

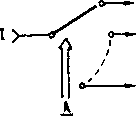
Rys. 5.14. Zasada działania i symbol demultipleksera

Zasadę działania demultipleksera ilustruje rys. 5.14, zaś na rys. 5.15 przedstawiono schemat demultipleksera o 8 wyjściach, którego wejściem informacyjnym może być np. G1, jeżeli G2A = G2B = 0.

Jak widać ze schematu, demultiplekser różni się od dekodera jedynie dodanym wejściem informacyjnym. Podanie na to wejście na stałe sygnału 1 (na rys. 5*15 G1 = 1, G2A = G2B = 0) zamienia demultiplekser w dekoder (z aktywnym zerem).

Demultipleksery, podobnie jak multipleksery, można łączyć dla otrzymania układu o większej liczbie wyjść. Przykład konstrukcji demultipleksera o 64 wyjściach przedstawiono na rys. 5.1&.