10643 Scan Pic0079

Ogniskowe soczewek, o których mowa w zadaniu, spełniają zależności:

_L_	£ I	11—* t—i
w	Kri	U h)

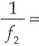
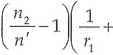
1_

Ej

gdzie ri jest bezwzględnym współczynnikiem załamania ośrodka, w którym zostały umieszczone obie soczewki. Dzieląc stronami oba równania otrzymujemy:

/i ₌ ⁿ2~ⁿ'

fz ⁿ\ -n'‘

Przyjmując, że ośrodek, w którym umieszczono soczewki jest optycznie rzadszy od obu rodzajów szkła, z których wykonano te soczewki, czyli ri Cttj i ri < n₂, mamy

4-* ^SM f\<fr

Rozwiązanie zadania 5.16 Prawidłowa odpowiedź: B.

Promienie padające równolegle do głównej osi optycznej soczewki 1 po przejściu przez nią przecinają się w ognisku, po czym jako wiązka rozbieżna padają na soczewkę rozpraszającą 2. Soczewkę rozpraszającą można potraktować w przybliżeniu jak dwa pryzmaty złączone wierzchołkami. Promień świetlny przechodząc przez pryzmat odchyla się zawsze ku jego podstawie. Tak więc wiązka rozbieżna po przejściu przez soczewkę rozpraszającą stanie się jeszcze bardziej rozbieżna.

Uwagi do zadań 5.17 - 5.25

Przy rozwiązywaniu kilku następnych zadań będziemy się posługiwać wzorem soczewkowym (patrz [4], str. 281). Wyraża on na ogół zależność odległościy obrazu od soczewki od odległości* przedmiotu od soczewki przy stałej ogniskowej / [dla oka y = const., a wzór soczewkowy wyraża zależność /(*)]. Wzór ten przedstawia się zwykle w postaci:

^x y f

W konkretnych przypadkach stosowania tego wzoru obowiązuje pewna konwencja dotycząca znaków występujących w nim wielkości*, y if I tak, jeśli przedmiot jest rzeczywisty, to przyjmujemy * > 0, jeśli uro-

jony (inaczej pozorny), to x < 0. Jeżeli obraz jest rzeczywisty, to przyjmujemy y > 0, jeżeli urojony, toy < 0. Jeśli soczewka jest skupiająca (ognisko rzeczywiste), przyjmujemy/> 0, jeśli jest ona rozpraszająca (ognisko urojone), to /< 0.

Wszyskie zamieszczone wyżej informacje dotyczą także zwierciadeł. Zwierciadło kuliste wklęsłe ma ogniskową/> 0 (ognisko rzeczywiste), zaś dla zwierciadła kulistego wypukłego/< 0 (ognisko pozorne).

Rozwiązanie zadania 5.17

Prawidłowa odpowiedź: C.

Dla soczewki płasko-wypukłej jeden z promieni krzywizny ma wartość

*0

. Zakładając, że drugi promień krzywizny ma długość

r₂ = R i korzystając z wzoru podanego w zad. 5.14 możemy w następujący sposób obliczyć ogniskową tej soczewki:

1 , 1 *•“ = (n -1)—,

/    R

ale ponieważ n- 2 to/= R.

Znając długość ogniskowej i odległość x = 2R przedmiotu od soczewki obliczymy z wzoru soczewkowego odległość y obrazu od soczewki:

— = — + — , skąd y = 2R. R 2R y

Powiększenie p wyraża się wzorem

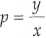
i w naszym przypadku równa się p = 1.

Rozwiązanie zadania 5.18 Prawidłowa odpowiedź: B.

Skoro uzyskany obraz jest pozorny, równanie zwierciadła ma postać:

Ze wzoru na powiększenie,

y

x

/    * V"