16021 IMG�79 (2)

s. =

z

j(*. -g)^ł

(n - 1)m

(1.13)

mianowniku wyrażenie n-I zamiast oczekiwanego n W ten sposób poprawia się przeciętną dokładność tych estymatorów, co może mieć znaczenie dla małych wartości n.

Gdybyśmy chcieli ocenić niepewność typu A wyniku pomiaru przyjętego jako średnia X za pomocą przedziałowej oceny (czyli przedziału ufności), to skorzystalibyśmy z zależności (1.14). Współczynnik k zależeć będzie od obranego poziomu ufności, ale tylko w

V-X±ks_i Ł    (1.14)

w przybliżeniu może być wyznaczony wg rozkładu normalnego (czyli w sensie podanym do 1.11 i 1.12). Nasza tu sytuacja jest inna niż w (1.11), ponieważ nie znamy dokładnie o, a korzystamy z estymatora    odchylenia standardowego cr_i, a nie z dokładnej wartości (T_i

Ze statystyki wiadomo, że odchylenie standardowe estymatora s (jest zmienną losową jako wynik działań na zmiennych losowych) jest odwrotnie proporcjonalne do -J2(n- 1) , co oznacza np. że dla w-10 wynosi prawie 24%. W miernictwie przyjmuje się, że niepewność ±24% oszacowania niepewności wyniku pomiaru jest zadowalającą dokładnością tego oszacowania. Gdy więc s jest wyznaczone z dziesięciu lub niewiele mniejszej liczby surowych wyników, to uważać powinniśmy, że określone jest dość dokładnie. Korzystanie wówczas z rozkładu normalnego i przybliżonej wartości s do wyznaczenia przedziału ufności jest zadowalająco dokładne. W przeciwnym razie - gdyby zależało nam na ścisłości i dokładności - współczynnik k trzeba by wyznaczać z rozkładu dokładniejszego w tej sytuacji - rozkładu zmiennej losowej I Studenta, mimo że nasza ocena X (jako zmienna losowa) ma rozkład normalny.

Przedziałowa miara niepewności typu A ma praktyczne zastosowanie tylko w okolicznościach, gdy niepewność typu 8 jest względnie tak mała, że może być pominięta. Ale wówczas oznacza to, że niepewność typu A jest tożsama z wypadkową niepewnością wyniku pomiaru. W przeciwnym razie estymator odchylenia standardowego s_£ (1.13) jest naturalną miarą niepewności typu A, którą trzeba złożyć z niepewnością typu B Gdy niepewność typu B jest też wyrażona za pomocą odchylenia standardowego, to składanie takie wykonujemy na zasadzie składania wariancji.

Sposób wyznaczania niepewności typu A jest - jak przekonaliśmy się - zalgorytmi-zowany, tj. istnieje rutynowy ciąg czynności doświadczalnych i czynności rachunkowych opartych na statystyce, prowadzących do celu. Nie istnieje odpowiedni algorytm do wyznaczania niepewności typu B. Pierwotne dane liczbowe potrzebne do oceny niepewności typu B otrzymujemy - jak to już wyjaśnialiśmy- bądź z danych o dokładności przyrządów użytych do mierzenia, bądź z dociekań, bądź tez dodatkowych eksperymentów i szacunków nieokreśloności wyniku pomiaru powstałych na skutek domniemanych przyczyn. Ogólnie od naszej dociekliwości zależeć będzie, czy dopatrzymy się powodu istnienia nieokreśloności wyniku i czy trafnie ocenimy liczbowo skutki działania danej przyczyny. Te pierwotne oceny liczbowe - otrzymane z dociekań - z zasady mają sens przedziałowy, o czym już mówiliśmy i co jest istotną ich cechą. Mają też jeszcze jedną cechę - otrzymujemy takie dane jako dane cząstkowe o niepewności typu B, ponieważ tych analizowanych przyczyn z reguły jest więcej niż jedna, a skutków ich nieokreśloności nie potrafimy ocenić globalnie

(łącznie), musimy wyodrębniać i oceniać każdy skutek z osobna Później te cząstkowe dane o niepewności typu B musimy złożyć, aby otrzymać wypadkową ocenę niepewności typu B Z obu wymienionych cech danych wyjściowych o niepewności typu B wynikają istotne następstwa Z tego, iż oceny liczbowe danych do wyznaczania niepewności typu B mają sens przedziałowy, a rodowód takich przedziałów może być różny, wynika, że nie potrafimy tych danych bezpośrednio złożyć w racjonalny sposób. Zadanie rozwiązuj* nę. gdy przedziałom nadamy sens przedziałów ufności o określonych przez nas poziomach ufności, przedziałów przypisywanych przez nas domniemanym zmiennym losowym o domniemanych przez nas rozkładach gęstości prawdopodobieństwa. W tym miejscu wprowadzamy więc do obiektywnych danych doświadczalnych subiektywność, a jej skutki zależne będą od stopnia naszej kompetencji. Dopiero w tych okolicznościach i w ten sposób potrafimy rozwiązać problem wyznaczenia wypadkowej składową niepewności typu B Z tak wprowadzonych subiektywnie założeń (typ rozkładu, przedział ufności, poziom ufności) możemy bowiem wyznaczyć wartości odchyleń standardowych (owych domniemanych zmiennych losowych), a odchylenia standardowe potrafimy już składać w sposób teoretycznie głęboko uzasadniony i uniwersalny.

Z zależności 6=-ko, w której Sjest pierwotną daną otrzymaną jako ocena cząstkową

s

o«—    (1.15)

k

lub wypadowej niepewności typu B, obliczamy - odwracając tę zależność - odchylenie standardowe tr(l 15). Taki rachunek powtarzamy dla każdego cząstkowego udziału składającego się na niepewność typu B Gdy przyjmiemy rozkład gęstości prawdopodobieństwa domniemanej zmiennej np. normalny i poziom ufności odpowiadający niepewności granicznej, to współczynnik k przyjmie wartość 3. Gdy przyjmiemy rozkład np. jednostajny (co asekuracyjnie często praktykuje się), współczynnik k przyjmie wartość V3 Przyjmując np. to ostatnie założenie sugerujemy tym samym, że rozrzut mieści się w przyjętym przedziale S, ale prawdopodobieństwo małych i dużych odchyleń jest jednakowe, a więc dla danego S odchylenie standardowe o będzie większe (konkretnie w tym przypadku V3 razy) niż gdybyśmy przyjęli rozkład normalny i k= 3. Oznacza to większy udział tą niepewności w dalszych szacunkach. Rozkład jednostajny często przyjmuje się przy ocenie skutków ograniczonej dokładności przyrządów, bo dla nich podawany jest błąd dopuszczalny, a o rozkładzie błędów wewnątrz tych granic możemy niewiele wiedzieć.

Z probabilistyki wiemy, że odchylenie standardowe sumy zmiennych losowych (niezależnych!) otrzymuje się jako pierwiastek z sumy kwadratów odchyleń standardowych składników (inaczej - sumy wariancji) i na tej podstawie dla niepewności typu B otrzymamy (1.16). Wskaźnik i oznacza, że sumujemy dla wszystkich m cząstkowych udziałów otrzymanych z oszacowania wpływu danego czynnika na wynik, czynnika wywołującego niepewność typu B

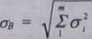
Zależność (1.16) otrzymaliśmy w szczególnych okolicznościach. Polegają one na tym, że niepewności cząstkowe o;, wywołane niepewnością określenia któregokolwiek udziału wyrażone były bezpośrednio w jednostkach tego samego wyniku pomiarowego, a nie w różnych jednostkach wielkości fizycznych, za pomocą których wyraża się dany czynnik naruszający dokładność. Jeżeli tak nie jest. to musimy skorzystać z prawa przenoszenia niepewności omówionego w następnym paragrafie.

Na tej samej zasadzie, na której otrzymaliśmy zależność (1.16), możemy złożyć niepewność typu A i niepewność typu B. W ten sposób otrzymamy zależność (1.17) wyra-

43