18435 wykad1036

Ir

Próbkowanie sygnału, twierdzenie o próbkowaniu, aliasing

W prawie każdym systemie cyfrowego przetwarzania sygnału występują dwie ważne operacje: próbkowanie i kwantowanie w celu zamiany sygnału analogowego ciągłego na sygnał cyfrowy

Próbkowanie

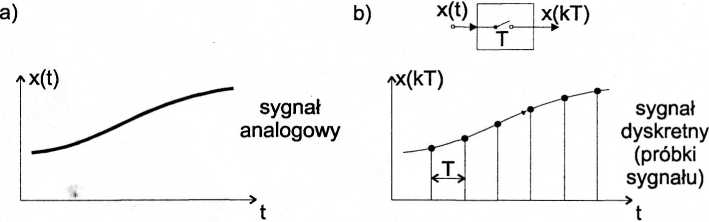
Okres próbkowania = T = T_p = T_s = T_próbkowania = T_sample-Częstotliwość próbkowania = fp = fg ⁼ ^próbkowania ⁼ ^sample ⁼ ”1 / "T. Przyjmuje się, że sygnał analogowy i jego próbki (sygnał dyskretny) są równoważne, gdy:

-    próbkowanie zachowuje charakter widma sygnału,

-    (teoretycznie) jest możliwe całkowite odtworzenie pierwotnego sygnału analogowego na podstawie jego próbek.

Dzięki stosowaniu filtru antyaliasingowego (na wejściu toru) przyjmuje się, że sygnał ma widmo o ograniczonym paśmie:

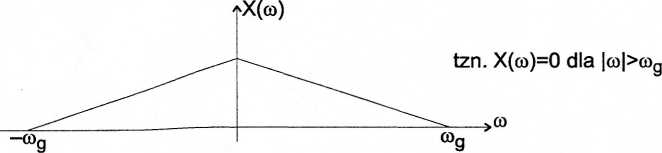
Obecność częstotliwości ujemnych wynika z właściwości transformaty Fouriera, która każdą rzeczywistą oscylację sinusoidalną o pulsacji co_k interpretuje jako sumę dwóch oscylacji zespolonych o pulsacjach co_k oraz (- co_k):

_TX(co)

-fi)g -ea_k

L

C£>-|

o>2

J-i->03

®k ®g

g

Transformata Fouriera j7^r{x(t)} sygnału sinusoidalnego x(t) = A-|Sin(a>-|t + (p-|) dla co > 0:

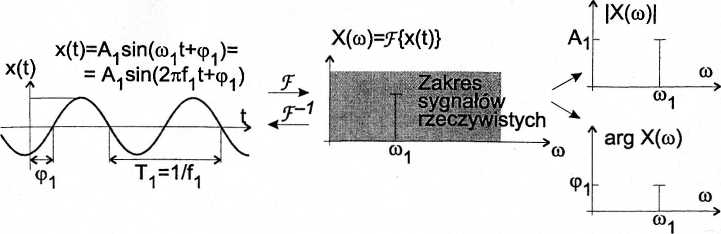
Transformata Fouriera J{x(t)} sygnału sinusoidalnego x(t) = A₁sin(co₁t + cp₁) dla co>0 oraz co<0:

1. Zapisanie oscylacji sinusoidalnej w postaci sumy dwóch drgań zespolonych na podstawie zależności sinx = (e^JX - e~^jX)/ 2j:

x(t) = A₁sin(co₁t +    = B₁e*^t“i^t + B^¹, gdzie: B-| =^le^Jtp1 jest amplitudą zespoloną oscylacji zespolonej B-ie^“^lt.

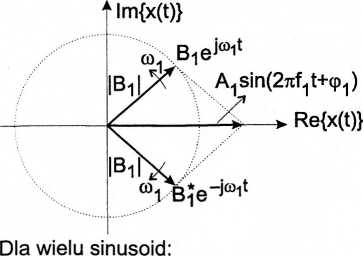
2. Wyznaczenie transformaty Fouriera przekształcającej sygnał z dziedziny zespolonej w dziedzinę zespoloną:

fX(eo)

X(co)

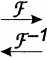
B-

co

CO.

-CO.

Dwa prążki odpowiadające dwóm sprzężonym ze sobą oscylacjom zespolonym dającym w sumie jedno drganie sinusoidalne