1tom257

10. TECHNIKA WYSOKICH NAPIĘĆ 516

daje dostatecznie duże prawdopodobieństwo, że izolacja będzie pracować prawidłowo w warunkach zagrożenia przepięciami o parametrach odpowiadających napięciom próby. Sposób przeprowadzenia próby zależy od jej charakteru i od rodzaju napięcia.

Próby napięciem stałym i przemiennym

Przy uwzględnieniu rodzaju badanej izolacji jest stosowane następujące postępowanie:

—    przyłożenie napięcia o wartości znacznie niższej (np. o ok. 30%) od przewidywanej wartości napięcia przebicia lub przeskoku;

—    podniesienie napięcia z ograniczoną szybkością (ok. 2% napięcia probierczego na sekundę) aż do osiągnięcia wartości probierczej napięcia lub do wystąpienia przeskoku (przebicia);

—    dokonanie pomiaru napięcia przeskoku przy co najmniej pięciokrotnym powtórzeniu próby.

Za napięcie przeskoku przyjmuje się wartość średnią U_p, obliczoną wg zależności (10.52), przy odchyleniu standardowym a_s z próby wg zależności (10.53) i przy wyznaczeniu przedziałów ufności na poziomie istotności ot zgodnie z zależnościami

cr_st(oc, n) ^P >

oyfot, n)

(10.13)

oraz

n—1    n-1

^(iai4)

gdzie: U_p — rzeczywista wartość napięcia; <r — odchylenie standardowe; n — liczba pomiarów; y,, y₂ i t(a, n)—zmienne losowe rozkładu y² i rozkładu Studenta wg rys. 10.19.

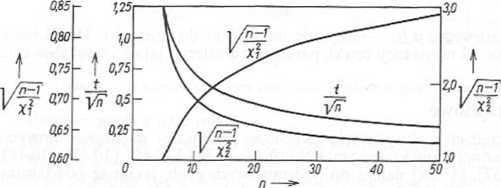
Rys. 10.19. Relacje pomiędzy zmiennymi losowymi r, y_v y₂ i liczbą pomiarów na poziomie istotności a = 0,05

W próbach izolacji napowietrznej należy uwzględnić wpływ warunków atmosferycznych wg zależności (10.43).

Próby napięciem udarowym

Do prób są stosowane udary ukośne (powodujące wyładowania na czole), udary piorunowe (pełne i ucięte) i udary łączeniowe.

Próby udarami ukośnymi o identycznej stromości narastania — prowadzące każdorazowo do przeskoku (przebicia) -— są podobne do końcowej fazy prób przy napięciu stałym i przemiennym z tym, że szybkość narastania napięcia jest znacznie większa (narzucona przez stromość udaru). Natomiast analiza wyników jest identyczna. Wielokrotne powtórzenie próby, uzupełnionej pomiarem czasu do przeskoku, przy zmianie stromości narastania napięcia (od możliwie największej do najmniejszej) pozwala na wyznaczenie charakterystyki napięciowo-czasowej.

Próby udarami piorunowymi pełnymi są stosowane do sprawdzenia odporności układu na napięcie probiercze (tabl. 10.14... 10.16) i do wyznaczenia tzw. metryki (50-procentowego napięcia przeskoku z odchyleniem standardowym) lub charakterystyki udarowej. Niekiedy wyznacza się też 0-procentowe napięcie przeskoku (badania konstrukcyjne izolacji nie regenerującej się) i 100-procentowe napięcie przeskoku (badania napięcia zapłonu ochronników). Napięcie probiercze doprowadzone do układu 3-t-5-krotnie nie powinno powodować uszkodzenia izolacji.

Metryka izolacji samoregenerującej się lub napięcie przeskoku na poziomie określonego kwantyla mogą być wyznaczone przy zastosowaniu metody serii (standardowej) lub metody „góra-dół”. W przypadku izolacji nic regenerującej się lub regenerującej się bardzo wolno jest przydatna schodkowa metoda Tetznera [10.29],

W metodzie standardowej do badanego układu doprowadza się kilka (nie mniej niż 4) serii po 10-f20 udarów jednakowego kształtu o napięciu na poziomie zbliżonym do 50% napięcia przeskoku. Amplituda udarów kolejnej (i-tej) serii jest zmieniana tak, by prawdopodobieństwo przeskoków P„ wyrażone stosunkiem ich liczby n, do liczby

11 udarów w serii, P, = — = /((/,), przyjmowało wartości rozłożone możliwie równomier-n

nie w' przedziale 0—1. Jak wynika z praktyki, rozkład ten jest zbliżony do normalnego. Korzystając z siatki funkcyjnej tego rozkładu i stosując metodę najmniejszych kwadratów, można wyznaczyć uśrednioną dystrybuantę P =f(fi) podaną na rys. 10.20 w skali liniowej

y = — lnJ [cr„ _s/2n f(0')]² jako prostą regresji

y = aU + b    (10.15)

przy czym

X ^utyi-ⁿu?

a = 4=^-, b = y—atj    (10.16)

Z Uf-niT-

i-1

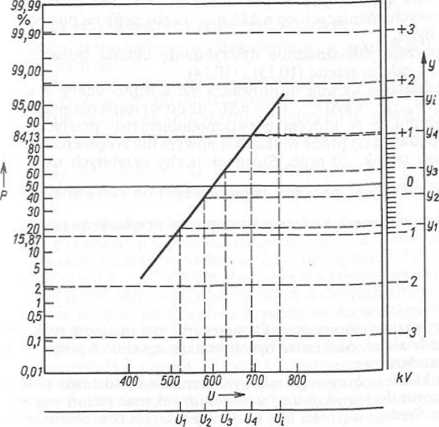
Rys. 10.20. Dystrybuanta P =/({/) w skali rozkładu Gaussa i prosta regresji y = /((/) w skali liniowej