23652 P1080231

4. Wprowadzenie do kinematyki robotów

punktu U

Rozwiązaniem układu równań będą współrzędne geometryczne xy_t y

(B₃s — D₃q)A\ -{B_xD₂-B₂D\)A₃

^ZU {-B₃r+C₃q)A_x ~(QB₂-C₂B_X)A₃

rz_u +s

yu =--

9

yu =—

(⁴-50)

B\y_u +C\z_u +D\

gdzie współczynniki q, r, s są określone równaniami

B₂-B_lA₂

r =

C₂ — C\A₂

A

(4.51)

s =

D₂-DiA₂

A

Mając współrzędne geometryczne xu,yu, ^zu punktu U, można wprost określić położenie chwytaka (współrzędne x_P, y_P, z_Pi). Punkt V leży na prostej prostopadłej do n₃ i przechodzącej przez punkt U, co wynika z geometrii mechanizmu, jakim jest manipulator o strukturze zamkniętej. Odległość Q₂V-1₂, VP = /₃. Ponieważ trójkąt Q₂UV jest prostokątny, więc przesunięcie punktu U do P można wyznaczyć według wzoru

(4.52)

d = UP = illl-(Q2(J)² +/₃

Rozwiązanie zadania odwrotnego manipulatora typu DELTA polega na wyznaczeniu zmiennych konfiguracyjnych (% (/= 1, 2, 3) jako funkcji pozycji i orientacji członu roboczego. Dla każdego ramienia manipulatora przyjmuje się układ współrzędnych X\ Y', Z\ przy czym oś Z' jest prostopadła do osi z głównego układu współrzędnych, a oś X' pokrywa się z osią silnika napędzającego rozpatrywane ramię. W nowym układzie współrzędnych każdego ramienia wyznacza się współrzędne punktu B, w zależności od współrzędnych punktu P{x_Pt yp, z/*) ze wzorów

(4.53)

\^xb\ ^{= x}p + Rb - Ra ¹ yai -yp ^zb\ ~^zp~h

Współrzędne punktu B, można wyrazić również w funkcji kątów a_h /?,, y_t

Ix_B\ = l\ coś a, - l₂ cosyi cos#

y_B\ =/₂sin/i    (4.5,

z_B\ = h sin ct\ +1₂ sin #

Z powyższych zależności wyznacza się kąty

P\ = arc cos

l\ cosai —x_B\ l₂ cos Y\

(4.55)

Wiedząc, że kąt y/ jest kątem dopełniającym do (a, + $) w płaszczyźnie ramienia, można go wyznaczyć ze wzoru

y/ = arc tg ft J    (4.56)

Do wyznaczenia kąta <p wykorzystuje się twierdzenie cosinusów dla trójkąta OjCjAj

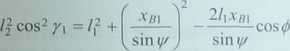
(4.57)

stąd można wyznaczyć kąt (f

<f> = arc cos

21\Xbi sin y/

(4.58)

Zmienną konfiguracyjną a\ można wyznaczyć ze wzoru

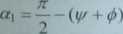
(4.59)

Podobnie wyznacza się zmienne konfiguracyjne cti i «3-

109