26200 PA274967

ANALIZA STATYSTYCZNA DANYCH

Cał\ proces w nioskowania statystycznego dotyczącego hipotezy zerowej p^. dzielić można na kilka etapów:    '    ^

•    Ustalanie schematu badania i liczby oraz sposobu pomiaru zmiennych zalej nych i niezależnych — jest to ściśle powiązane ze stawianymi pytaniami i hipo. tezami badawczymi;

•    Formułowanie hipotezy zerowej - wiąże się automatycznie z wyborem testu statystycznego;

•    Sprawdzenie założeń wybranej techniki statystycznej;

•    Obliczenie wartości statystyki testu według ustalonej procedury (wzoru)-ru szczęście robi to za nas program statystyczny, taki jak np. SPSS;

•    Odczytywanie wartości krytycznych dla danej statystyki z tablic statystycznych, odnoszenie otrzymanej wartości testu do ustalonego poziomu istotności - jakby strasznie to nie brzmiało, też robi to za nas program typu SPSS;

•    Podjęcie decyzji o odrzuceniu bądź nie hipotezy zerowej;

•    Interpretacja wyników; najczęściej na podstawie dodatkowych statystyk opiso-wych.

Błąd pierwszego rodzaju

Weryfikacja, a więc potwierdzenie lub odrzucenie przypuszczeń polega na obliczeniu, na podstawie uzyskanych z próby (czyli grupy przebadanych osób) da-nvch, tego, jakie jest ryzyko, że odrzucana przez nas hipoteza zerowa w rzeczywistości jest prawdziwa (mamy tu do czynienia z tzw. błędem pierwszego rodzaju). Postępujemy w ten sposób, ponieważ wyciągamy wnioski na podstaw dostępnej nam próby, a nie całej populacji*.

W badaniach psychologicznych dopuszczalny poziom błędu pierwszego rodzaju (czvli rvzvka zanegowania/odrzucenia prawdziwej hipotezy zerowej) to 5% (inaczej zapisane 0,05). Jeśli w obliczanym teście uzyskane prawdopodobieństwo wynosi 5 lub mniej procent, mówimy, że test jest istotny statystycznie. I zapisujemy jako p < 0,05 (co można odczytać jako „prawdopodobieństwo popełnienia błędu I rodzaju jest mniejsze niż 5%”). Jeśli prawdopodobieństwo to jest dużo mniejsze niż pięć procent, możemy dać temu wyraz w zapisie wyruku stosując progi 0,01 lub

¹ Warto dodać, że populacja w statystyce to dowolna grupa liczb, skończona lub nieskończona, odnosząca się do rzeczywistych lub hipotetycznych obiektów lub zdarzeń. Zwykle, jako badacze, stykamy się tylko z próbkami, czyli cząstkami interesujących nas populacji. Podczas oceny rezultatów eksperymentu pytamy na przykład: czy dwa zbiory wyników rzeczywiście sif różnią? Tak naprawdę interesuje nas stwierdzenie, czy pochodzą one z różnych populacji (różnią się), czy^r z tej samej (nie różnią się). Ponieważ próbka zazwyczaj nie jest dokładnie reprezentatywna w stosunku do swej populacji, nigdy nie możemy być całkowicie pewni, czy nasze wnioski są w stu procentach prawidłowe - stąd konieczność podejmowania decyzji z pewnym prawdopodobieństwem popełnienia błędu. Gdy przeprowadzamy eksperyment, zazwyczaj losujemy jedną próbkę, którą następnie dzielimy na dwie (albo więcej), z czego jedną z nich poddajemy manipulacji eksperymentalnej. Jak tu mówić o wynikach pochodzących z różnych populacji? Tu pojawia się dosyć istotna kwestia związana z traktowaniem próbek przez statystyków (w tym programy statystyczne). Dla celów statystycznych nasza próbka staje się populacją wyników a nie populacją obiektów. I jeśli działania eksperymentalne się powiodą — dwiema populacjami wyników. Programy statystyczne traktują wpisane liczby jako pochodzące bezpośrednio z jednej albo z dwóch populacji - czyli „populacja” to nic innego jak „zbiór liczb”.

₇. WNIOSKOWANIE STATYSTYCZNE NA DANYCH JAKOŚCIOWYCH..,

oool. Jeśli wynik zawiera się w przedziale od 0,05 do 0,1 (czyli między pięć a dziesięć procent), mówimy o tendencji w istotności. Gdy wynik testu jest nieistotny statystycznie (prawdopodobieństwo popełnienia błędu pierwszego rodzaju większe _niż 10 procent) posługujemy się zapisem ni. (skrót od „nie istotne”).

Podczas weryfikacji hipotezy zerowej napotykamy ryzyko popełnienia dwóch błędów -1 i II rodzaju:

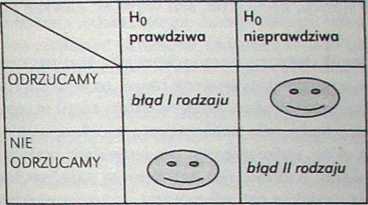
Odrzucając prawdziwą H₀ popełniamy błąd I rodzaju, natomiast nie odrzucając fałszywej H₀, popełniamy błąd II rodzaju.

Ryzyko (prawdopodobieństwo) popełnienia błędu I rodzaju nazywane jest poziomem istotności — w badaniach staramy się zminimalizować to ryzyko.

Błąd // rodzaju

Co ważne - nieistotny wynik nie oznacza tego, że hipoteza zerowa jest prawdziwa- jest to pewien skrót myślowy. Na tej podstawie możemy powiedzieć jedynie, że nie udało nam się w trakcie postępowania badawczego odrzucić hipotezy zerowej i tym samym wykazać prawdziwości hipotezy badaw-czej — i to wszystko, co możemy wywnioskować. Jak się okaże w dalszej części tego rozdziału, nie zawsze (chodaż oczywiście najczęściej) dążymy do sytuacji, w której test jest istotny statystycznie - w pewnych przypadkach — gdy np. sprawdzamy niektóre założenia testów - dążymy do wyniku nieistotnego statystycznie i nie odrzucania hipotezy zerowej danego testu. Ale, jak już powiedzieliśmy, są to przypadki specyficznego użycia testów.

Jak zapisać poziom istotności testu:

p < 0,001 - jeśli wartości p nie przekraczają 0,001 p < 0,01 - jeśli wartości p zawierają się vv przedziale od 0,001 do 0,01 p < 0,05 - jeśli wartości p zawierają się w przedziale od 0.01 do 0,05 dokładna wartość p — jeśli wartości p są od 0,05 -0,1 (tendencja, np. p < 0,052)

ni. - jeśli wartości p są powyżej 0,1 — wynik nieistotny