31431 P3310036 (2)

d

IK

su,

(4 17)

którego licznik jest metryką miejską, zaś mianownik można traktować jako miarę ląc znc) wielkości dwóch obiektów (zob. Anderberg, 1973). Jest to zatem również pewna odmiana metryki miejskiej i uogólnienie odległości Czekanowskiego²⁴. Niezależnie od tego współczynnik ten jest uogólnieniem współczynnika Dice’a, niemniej nie jest on miarą metryczną²⁵.

Zarówno metryka Canberra, jak i współczynnik Lance'a i Williamsa są żale cane dla danych cechujących się skośnością oraz występowaniem wartości skrajnych (zob Tintm, 2002).

• Współczynnik dywergencji (ang. coejficient of divergence)

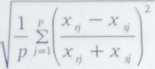
(4.18)

użyty po raz pierwszy przez Clarka w 1952 roku na gruncie biologii. Przybiera on wartości z przedziału [0,1], a przez to jest stosowany dość często (zob. Sneath i Sokal, 1973).

• Miara odległości Matusity²⁶

(4.19)

Metryka Gowera

(4.20)

²⁴    Miara to bywa też nazywana współczynnikiem Czekanowskiego (zob. Timm, 2002). Co do na rwy tego współczynnika, to nie ma pełnej jasności - czasami jest on przypisywany Rrayowi i Curti sowi (zob. Janowitz, 2002).

²⁵    Jeżeli współczynnik I.ancea i Williamsa zastosujemy do zmiennych binarnych (0 - 1), to otrzymamy dopełnienie współczynnika Dice’a do 1, ponieważ X ^ — x_<|= b + c oraz

X + •*,) “ (a+ b)+ (<t+ r)(zob. punkt 4.4.3).

26    Miara ta jest też. nazywana odległością łlellingera (zob Gordon. 1999).