34210 skanuj0505

niom refleksów o bardzo dużej wartości 26 (refleksy zwrotne). Można udowodnić teoretycznie, że niektóre błędy zniekształcające systematycznie pomiary parametrów znikają, gdy 26 = 180°. Ze względu na to w oznaczeniach, w których wymagana jest duża dokładność, przeprowadza się ekstrapolację do 180° pomiarów wyprowadzonych z obserwacji odpowiadających wartościom 26 zbliżającym się coraz bardziej do 180°.

Pomiary przeprowadzone za pomocą dyfraktometrów umożliwiają łatwiejsze wyznaczenie dokładnych wartości parametrów sieci, na ogół więc posługujemy się tymi przyrządami po wstępnym przebadaniu sieci przy użyciu błony fotograficznej.

C. Wyznaczanie grupy przestrzennej

Po ustaleniu symetrii Lauego konieczne jest zestawienie wygaszeń systematycznych (s. 433). Mogą one niekiedy określać grupę przestrzenną w sposób jednoznaczny. Tak na przykład kryształ jednoskośny (na co wskazuje jego klasa Lauego), który wykazuje

następujące wygaszenia:
w hkl	brak	(a więc sieć P)
w hOl	/ = 2n	(płaszczyzna c)
w 0&0	k = 2n	(oś 2t)

musi należeć do grupy P2₁/c. Natomiast kryształ jednoskośny nie wykazujący w swych widmach żadnego systematycznego wygaszenia mógłby należeć do grup P2, Pm lub P2jm.

Gdy wygaszenia nie określają grupy przestrzennej w sposób jednoznaczny, stosuje się pewne teksty, które mogą usunąć niejasność. Oto najczęściej używane spośród nich:

1) analiza statystycznego rozkładu natężeń (w praktyce przyjmuje się, że natężenia te zostały już zmierzone); można udowodnić teoretycznie (Howells, Phillips i Rogers), że ułamek N(z) refleksów, których natężenia są mniejsze lub równe iloczynowi z i natężenia

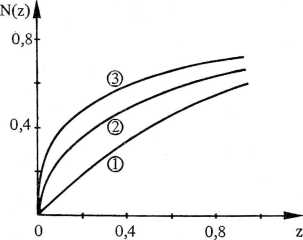
Rys. 4.90. Rozkłady: 1 — acentryczny, 2 — centrycz-ny, 3 — hipercentryczny

średniego </₀>, przybiera różne wartości (rys. 4.90), zależnie od tego czy struktura ma, czy też nie ma środka symetrii, a także od tego, czy struktura ma ponadto środki symetrii niekrystalograficzne (rozkład hipercentryczny); średniej </₀) nie oblicza się dla zbioru refleksów widma, lecz odpowiada ona każdej grupie refleksów należących do danego zakresu sinS, co wyjaśniono na s. 510;

507