41476 skrypt006

9

s - odchylenie standardowe,

t - parametr rozkładu Studenta zależny od przyjętego poziomu ufności (zwykle przyjmowany jako 0,95 - I - a); gdzie a jest poziomem istotności.

2.2. METODY REGRESJI I KORELACJI

Analiza regresji i korelacji jest zaawansowaną metodą obróbki wyników badań, w przypadku występowania zmiennych losowych. Analiza regresji pozwala na wyznaczenie związku między wartościami średnimi dwóch zmiennych. Zależność ta może być liniowa i wówczas mówimy o regresji liniowej. Funkcją regresji może być również dowolną funkcją nieliniową i wówczas określamy ją jako regresję nieliniową. Należy zaznaczyć, że przy wyborze funkcji należy kierować się przesłankami fizycznymi zmian badanej cechy. Regresja wielokrotna to zwykle funkcja liniową wielu zmiennych. Do wyznaczenia funkcji regresji używa się najczęściej metody najmniejszych kwadratów. Polega ona na takim doborze parametrów- aproksymowanej funkcji, aby suma kwadratów odchyleń rzędnych punktów empirycznych od wykresu tej funkcji była najmniejsza. Metodę tę dobrze ilustruje przypadek regresji liniowej, dla którego funkcję przewidujemy w postaci równania:

A

(Ml

y = ax + b

Zasada najmniejszych kwadratów narzuca warunek (1.5):

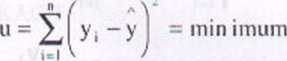
gdzie: y, - wartość zmiennej losowej.

Przedstawiona zależność jest funkcją współczynników a i b. a więc dla minimalizowania sumy należy ją zróżniczkować po a i b i wynik przyrównać do zera. Z zależności tych otrzymujemy wartości współczynników- a i b. Odpowiednie wzory przyjmują postać:

a =

n

ii

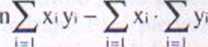
II

II

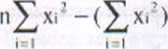
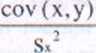
(i 6}

(1.7)

b = y - a x