51088 Untitled Scanned 19 (8)

2. PLANIMETRIA

CZĘŚĆ TEORETYCZNA

KĄTY

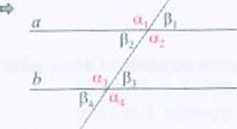
Jeśli proste a i b są równoległe, to a_l~((_: = u_K=a_l i

«,    i    a_v    «, i    cr₄,    i [i_:, fi₃ i fi₄ - kąty wierzchołkowe

u_t    i    u, i    a_v    /), i //,. /?, i /F - kąty odpowiadające

a_:    i    a_y    /f_: i    /[,    kąty nuprzemianlcgłc (wewnętrzne)

TWIERDZENIE TALESA

=$ Jeżeli ramiona kąta przetniemy prostymi równoległymi, to odcinki wyznaczone przez te pioste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.

Jeżeli m II ii, to

\oa\ Mfll m koi

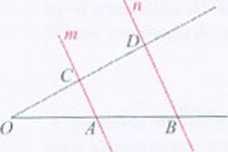
TRÓJKĄT

UWAGA. We wszystkich wzorach i twierdzeniach dotyczących trójkąta przyjmujemy. ?c

I > naprzeciw kątów <> miarach a. /!. y leżą hnki o długościach od|\iwicdnio o, b. c.

2.i r oraz. K są promieniami okręgów odpowiednio wpisanego w trójkąt i opisanego na trójkącie. ^ T rójkąt prostokątny o pr/.yprostokątnych a. b i przeciwproslokątnej e.

Funkcje trygonometryczne w trójkącie prostokątnym:

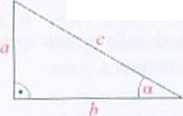
sinrr=—,

r

cosrx=—. c

Twierdzenie Pitagorasa: a' 4- b = <\ Fole: I> = \ab.

T rójkąt równoboczny o boku a.

Pole: P =

_R=i_h=“£,

<=c> Cechy podobieństwa: kąt-kąt, hok-kąt-bok, bok-bok-bok.

Pole: P-^ah, P = ~absiny. P = \rui + b + r), r = ~.

& Środkową nazywamy odcinek łączący wierzchołek ze środkiem przeciwległego boku.

Środkowe przecinają sic w jednym punkcie, zwanym środkiem ciężkości trójkąta.

Punkt ten dzieli każdą środkową w stosunku 2:1.

ł>wusieozne kątów (wewnętrznych) przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w trójkąt.

Symelralnc boków przecinają sic w jednym punkcie, który jest środkiem okręgu opisanego na ttójkącic.

=?* Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego i równy jego połowie.

=> Twierdzenie sinusów: —— =    — = 2K.

mu &    sin p    sin;"

■4- Twierdzenie kosinusow: c² = o' 4- 2 ab COS y.

Wysokość: h = ^.

‘jlA

4

*> Twierdzenie o dwusiecznej kata w trójkącie.

Dwusieczna kąta trójkąta dzieli przeciwległy bok na odcinki, których stosunek długości jest równy stosunkowi długości pozostałych boków: — = .