53432 skanuj0271 (4)

Graniczna liczba zębów. Analizując współpracę narzędzia — zębatki z kołem obrabianym, określono najmniejszą liczbę zębów, przy której nie wystąpi jeszcze podcięcie.

Teoretyczną graniczną liczbę zębów z_g oblicza się z zależności

sin² a₀

(11.21)

Gdy z < z_g, występuje podcięcie zęba u podstawy. Ponieważ w praktyce dopuszcza się nieznaczne podcięcie nie powodujące jeszcze ujemnych skutków, wprowadza się praktyczną graniczną liczbę zębów ź_g, określoną zależnością

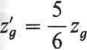
(11.22)

Dla podstawowych kątów przyporu graniczne liczby zębów wynoszą: dla a₀ = 20° jest z_g = 17 oraz z'_g = 14 dla cc₀ = 15° jest z_g = 30 oraz z'_g = 25

Należy nadmienić, że w wyniku nacinania zębów narzędziem w kształcie koła (metodą Fellowsa) graniczne liczby zębów są nieco mniejsze.

Przesunięcie zarysu zęba. Dążenie do stosowania urządzeń o niewielkich wymiarach powoduje m.in., że koła zębate o liczbie zębów mniejszej od granicznej są dość często stosowane. Aby jednak uniknąć podcinania tych zębów, wykorzystuje się niewrażliwość zarysów ewolwentowych na wzajemne ustawienie kół i stosuje się dodatnie przesunięcie zarysu zęba, polegające na tym, że przy nacinaniu uzębienia narzędzie odsuwa się od koła nacinanego o wartości X (rys. 11.14). Wartość przesunięcia zarysu X zależy od liczby zębów oraz jest proporcjonalna do wartości modułu. W celu uniezależnienia obliczeń przesunięcia zarysu od wartości modułu wprowadza się współczynnik przesunięcia zarysu x

X

x = —

m

(11.23)

stąd X = x • m

Współczynnik przesunięcia zarysu x ustala się z zależności

a) x — ———    lub b) x — ———    (11-24)

^Z9    ^Z9

Wersję a) stosuje się przy założeniu, że nawet minimalne podcięcie zarysu jest niedopuszczalne, natomiast wersję b) — w przypadku dopuszczalnego niewielkiego podcięcia zarysu.

Współczynnik * przesunięcia zarysu może przybierać wartości w zakresie: — 1 < jc < +1. Oznacza to, że w kołach o dużej liczbie zębów można stosować ujemne przesunięcie zarysu, czyli wsunięcie narzędzia w głąb koła, przy czym średnice koła (d_a i d_f) są wówczas zmniejszone o wartość 2X.

271