57224 Untitled Scanned 29 (8)

grupowymi. Zawsze możemy znaleźć takie dwie wartości X_t i X₂, aby wyrazić każdą wartość reakcji odrzuconych więzów. Liczba niewiadomych przy tym sposobie ich wyrażania nie ulega zmianie.

W przykładzie pokazanym na rys. 13.31 dzięki symetrii wykresu A/j i antysymetrii M₂ otrzymamy S₁₂=S₂₁—0.

f) -Trrfflllffl	r&r.
	jttmt §§§
	=
*

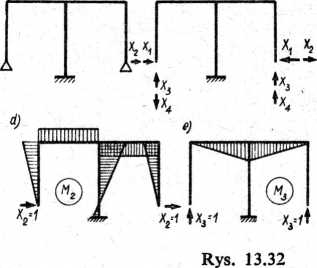
Weźmy jeszcze pod uwagę ramę pokazaną na rys. 13.32a. Rama jest 4-krotnie statycznie niewyznaczalna. Układ podstawowy pokazano na rys.13.32b, a wartości przemieszczeń w równaniach kanonicznych metody sił w poniższej macierzy (znak V oznacza niezerową wartość przemieszczenia):

Lp.	Xl	x2	X3	X*
1	V	0	V	0
2	0	V	0	V
3	V	0	V	0
4	0	V	0	V

Spośród 16 wyrazów macierzy aż 8 przybiera wartości zerowe, co daje znaczne uproszczenie przy rozwiązywaniu. Oczywiście wszystko, co powiedzieliśmy w tym punkcie, dotyczy tylko układów symetrycznych.    *

13.6.6. Stosowanie różnych układów podstawowych

Następnym ze sposobów umożliwiających niekiedy uproszczenie obliczeń wartości przemieszczeń S_ik oraz A_ip jest korzystanie przy rozwiązywaniu jednej i tej samej ramy z różnych układów podstawowych (oczywiście geometrycznie niezmiennych i statycznie -yznaczalnych). Możemy więc dla sporządzenia wykresu momentów, np. M-_t od obciążenia X_t (równego jedności lub dowolnej innej - wygodniejszej wartości), skorzystać i jednego spośród możliwych dla danej ramy układów podstawowych, natomiast dla otrzy-rcania np. M_k - posłużyć się innym układem podstawowym. Podobnie dla sporządzenia kresu M_p możemy wykorzystać jeszcze inny układ podstawowy. Dobierając dla jednej

467