66360 S6303026

422 HYDRAULIKA TECHNICZNA. PRZYKŁADY OBLICZEŃ

Związek ten pozwala na wyznaczenie skal innych wielkości fizycznych w funkcji skali długości:

skala prędkości:	a -a-*'* ^av “ 3/2 ^aL cl, a^3/^2	(15.69)
skala przepływu:	^aQ ^=av^aA =al^1/2«l =ai'^2	(15.70)
skala siły:	aF =aaaL =aL	(15.71)
skala ciśnienia:	olf aL _j a =-^=-f=aj P a i	(15.72)
skala pracy:	aw =aFaL =cl^2l	(15.73)
skala mocy:	a -^al -a^ ^A a, a l^12	(15.74)

Kiyterium Webera oparte na zachowaniu wzajemnego stosunku sił wynikających z napięć powierzchniowych i sił bezwładności zapewnia właściwe odwzorowanie tych zjawisk, w których decydujące znaczenie mają siły napięcia powierzchniowego. Dotyczy przede wszystkim zjawisk podsiąkania wody w gruncie oraz badań właściwości kropel.

Możliwość odwzorowania zjawisk hydraulicznych przy jednoczesnym modelowaniu różnych sił

Dotychczas omówiono kryteria podobieństwa, dzięki którym możliwe było modelowanie sił: ciężkości (kryterium Froude’a), tarcia (kryterium Reynoldsa), sprężystości (kryterium Cauchy’ego) oraz napięć powierzchniowych (kryterium Webera). Każde z powyższych kryteriów wymaga spełnienia innych skal podobieństwa w odniesieniu do tych wielkości fizycznych, które najbardziej nas interesują (jak np. prędkość, natężenie przepływu, czy ciśnienie).

Teoretycznie możliwe jest przeprowadzenie badań modelowych przy jednoczesnym zastosowaniu czterech kryteriów podobieństwa.

W tym celu należałoby rozwiązać układ równań:

a_F = a_pa;a²L = a_pa_ga* = aja"¹ = a^a \ = a₀a_L (15.75)

siła    siła    siła    siła    napięcie

bezwładności ciężkości    lepkości    sprężystości powierzchniowe

Podane równanie wiąże siedem różnych skal.

Przy dowolnych skalach CC_g, 0^,0^, CC c, 0C_o niemożliwe jest dobranie realnych skal

długości i prędkości, które jednoznacznie spełniałyby wyżej wymienione równania. Gdy pominie się jeden z warunków, ale nie Froude’a, to układ staje się rozwiązalny, lecz wymaga modelowania siły masowej g. Dopiero rezygnacja z podobieństwa dwóch

Projektowanie parametrów geometrycznych i hydraulicznych fizycznego modelu 423

rodzajów sił i jednoczesne zachowanie tylko dwóch pozostałych kryteriów umożliwia przyjęcie a_ = 1, choć stwarza to konieczność wprowadzenia innej cieczy na modelu niż

w naturze.

Rozpatrzono też przypadek jednoczesnego zastosowania kryterium Froude’a i Reynoldsa (który jest najbardziej realny w modelowaniu hydraulicznym). Skalę prędkości według kryterium Froude’a wyraża zależność

H | ot¹/²    (15.76)

a według kryterium Reynoldsa:

a, = a_va^    (15.77)

Aby spełnić jednocześnie oba powyższe kryteria, musi zachodzić warunek:

a'/² = a_va|    (15.78)

czyli:

<x_v

= a:

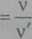
(15.79)

Spełnienie ostatniego warunku oznacza w praktyce zastosowanie na modelu cieczy, dla której kinematyczny współczynnik lepkości będzie wielokrotnie mniejszy niż cieczy w naturze (najczęściej wody). Na przykład przy skali geometrycznej a_L = 1/10 oznacza to konieczność użycia cieczy 33-krotnie mniej lepkiej niż woda, co jest mało realne. Wobec ograniczonej liczby cieczy o różnych lepkościach do modelowania dobiera się •    v

wstępnie właściwą ciecz i ze stosunku — wyznacza się dopiero skalę geometryczną

v

modelu. Taki sposób postępowania sprawia, iż często geometryczna skała modelu nie stanowi „okrągłej” liczby (np. a_L =1/124). Łatwo też zauważyć, że jednoczesne spełnienie kryterium Reynoldsa i Froude'a przy zastosowaniu tej samej cieczy na modelu i w naturze (a_v =1) prowadzi do wniosku, iż jedyną skalą geometryczną spełniającą warunek wyrażony zależnością (15.78) jest a_L =1. Oznacza to, że model jest wielkości naturalnej. Na takim modelu oba powyższe kryteria podobieństwa zostają całkowicie spełnione. Model wykonany w skali 1:1, jako wierne odwzorowanie warunków naturalnych, spełnia oczywiście jednocześnie wszystkie prawa podobieństwa. Modelowanie zjawiska hydraulicznego według jednego warunku podobieństwa daje możliwość dowolnego założenia podstawowej skali modelu. Jest nią zwykle skala geometryczna, która wynika z możliwych do realizacji rozmiarów modelu, lub skala przepływów (wynikająca z wydajności pompowni).

Podobieństwo całkowitych oporów ruchu. Skażenie modelu

Ważne miejsce w badaniach hydraulicznych zajmują przepływy w korytach otwartych.

Koryta te mogą mieć dno stałe (nierozmywalne) lub rozmywalne.