68798 MATEMATYKA167

324 VI. Ciągi • sten#funkcyjne

324 VI. Ciągi • sten#funkcyjne

(4.2)

a„ = ljf<x)cos^dx dla n=0,l,2.....

b_n*| jf(x)sin-pdx dla n = 1,2,3.....

W szczególności, gdy t = rc otrzymujemy szereg trygonometryczny postaci

w

(4.3)

-i+£(a_n^cosnx + b_n^smnx)

B«l

Jeżeli len szereg jest zbieżny na przedziale < -Tl, 7t >,to jest on zbieżny na zbiorze R i suma tego szeregu jest funkcją okresową o okresie 271.

TWIERDZENIE 4.1' Jeżeli szereg trygonometryczny (4 3) jest jednostajnie zbieżny na przedziale < —n, n > i jego suma jest równa f(x), to współczynniki a_n i b_n są określone wzorami Eulera - Fouriera

n

a„ = — Jf(x)cosnxdx dla n=0j,2,...,

-»

X

b_n =--Jf(x)sinnxdx dla n = l,2,3,....

1

(4.4)

Dowód. Sumą szeregu (4.3) jest funkcja f(x), więc:

Xi

(a)    f(x) = ~+£(a„cosnx + b_nsinnx) dla <-7i,n>.

Szereg ten jest jednostajnie zbieżny na przedziale < -tt.ti >, w ięc można go całkować wyraz po wyrazie (tw. 2.1 rozdz. VI) na przedziale < — ii, 7i >, to znaczy

n    n m h    n

(b) J f(x)dx ~~2 J dx £(a_n Jcosnxdx+b„ Jsinnxdx).

■    n    -*    «

Ponieważ

i    x    . n    *

Jdx = 2x, Jcosnxdx = -ⁿ^    =(), Jsinnxdx = 0.

-X    -n    n

więc z równości (b) otrzymujemy

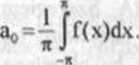
Niech k oznacza dowolnie ustaloną liczbę naturalną Wyprowadzimy wzór na współczynnik a_k, k = l,2,.„ Mnożąc obie strony równości (a) przez cos kx otrzymujemy

(c)    f( x)coskx=y coskx +2 (a_n cosnxcoskx+b_n sin nxcoskx).

Wykazuje się, że szereg w równości (c) jest też jednostajnie zbieżny, zatem

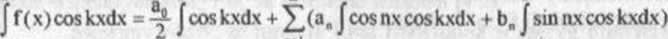
-r    -*    i»³'    -«    -■

Uwzględniając teraz, że

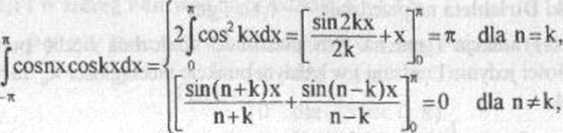
n

j*sinnxcoskxdx = { całka na przędz. <-x,x> z funkcji nieparzystej }=0

n

otrzymujemy równość

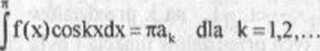
-H

Wzór na współczynniki b_k wyprowadza się, analogicznie jak na

współczynniki a_k, mnożąc obie strony równości (a) przez sin kx. fi

Uwaga I. Jeżeli f jest funkcję nieparzysty nu przedziale <-x,x>, (u wszystkie współczynniki n_n we wzorze (4.4) są równe 0

Uwaga 2 Jeżeli f jest funkcją parzysty rui przedziale <-x.x>, to wszystkie współczynniki b_n we wzor/e (4 4) są równe 0.

Uwaga 3. Jeśli f jest funkcją okresową o okresie 2x. to całki oznaczone nu przedziale <-x,x> we wzorze (4 4) można zastąpić całkami oznaczonymi na przedziale <0,2x>:

a,

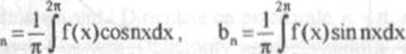
o

o