72715 S6303032

434 HYDRAULIKA TECHNICZNA. PRZYKŁADY OBLICZEŃ

Równania algebraiczne zapisane dla układu współrzędnych prostokątnych obranego w sposób pokazany na rysunku 15.4 (przy pominięciu ciężaru cieczy zawartej w objętości kontrolnej) mają postać:

^Pl'x - ^P2x ~^Px= PQ(^Vlx ~^Vx) /?' =0 stąd:

R = R_X =Ą'-^pź-pQ{v'_l-v')

/?=! 19 m • 1,5 m -

(24)

(25) (26) (27)

m

-1000-^f--80,47

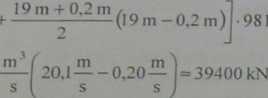
m

(l 9 m — 0,2 m ) I • 9810    • 20 m —

(28)

W warunkach naturalnych na przelew działa parcie dynamiczne równe wartości reakcji hydrodynamicznej lecz przeciwnie skierowane P_d = 39400kN .

Znając wartość siły parcia dynamicznego działającego na przelew w warunkach naturalnych obliczono wartość siły parcia dynamicznego działającego na model przelewu:

(29)

PRZYKŁAD 15.4.

Pewna charakterystyczna prędkość na przelewie wynosi v — 3m/s. Model przelewu zostanie z wymiarowany na podstawie kryterium Froude’a. Jaka powinna być geometryczna skala modelu a*., która zapewni wartość liczby Webera na modelu We =100 przy założeniu stałej temperatury wody na modelu i przelewie t' = 20°C ?

Liczba Webera definiowana jest jako stosunek siły bezwładności do siły napięcia powierzchniowego:

oL a

gdzie a - napięcie powierzchniowe cieczy [N/m]

Stosunek liczby Webera na modelu i prototypie przelewu określa zależność:

pLv^z

JVe _ g _    £2)

We⁷ p'l/v'^a a„ o'

Po przyjęciu wartości skal <x_p = 1, a₀ = 1 oraz uwzględniając, że według kryterium Froude’a a_v = a¹/², otrzymano:

We _	/ i/a\z 2
We'"	7
stąd:	[We*
%=•»	Iw

(3)

(4)

kg/m³ oraz

Podstawiając gęstość wody w temperaturze / = 20°C równą p = 998 napięcie powierzchniowe wody a = 0,0728 N/m otrzymano:

100

998kg/m³ ■ 10m• (3m/s)² 0,0728 N/m

= 0,0090028=— 111

(5)

Oznacza to, że na modelu przelewu wartość liczby Webera osiągnie 100, gdy geometryczna skala modelu będzie a_L = 1:111.