77483 P3200157

242 i^nalizask^eń

3) w przypadku zmiennej binarnej pożądane jest wykluczenie skojarzeń nega tywnych (współ-nieobecności, kategoria „nie-nie”) (0).

W celach ilustracyjnych posłużmy się następującym przykładem (4.1).

Przykład 4.1. (współczynnik Gowera)

Załóżmy, że w badaniu opinii publicznej uzyskano następujące informacje od respondentów:

Respondent	Wiek	Stopień poparcia dla...	Czy ma obecnie pracę	Czy brał udział w ostatnich wyborach	Samoocena stopy życiowej
Respondent 1	25	Średni	Nie	Nie	Bardzo niska
Respondent 2	36	Niski	Nie	Nie	Niska
Respondent 3	22	Wysoki	Tak	Tak	Przeciętna
Respondent 4	47	Wysoki	Tak	Nie	Przeciętna
Respondent 5	41 | Umiarkowany		Tak	Nic	Wysoka

Przyjmijmy, że z punktu widzenia badanego problemu wszystkie zmienne są istotne (w_{n (} = 1 dla wszystkich jakkolwiek badacz chce wyłączyć wpływ tylko negatywnych połączeń odnośnie do zmiennej: „uczestnictwo w wyborach” na ocenę podobieństwa respondentów, będąc przekonanym, że w większym stopniu o podobieństwie decyduje uczestnictwo w głosowaniu niż nieuczestniczenie. W takiej sytuacji w_ni =0 dla /= 4, jeśli takie negatywne połączenie (nie-nie) wystąpi dla jakiejś pary respondentów . Współczynnik Gowera obliczony dla pary respondentów (1,2) przyjmie wartość

Dla paru respondentów (1,3) będziemy natomiast mieli

l+l+l+l+l

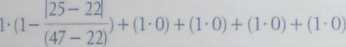
= 0,176

itd. Dla wszystkich par respondentów macierz podobieństwa jest następująca: ⁵⁵ Zob. dyskusję w punkcie 4.3.3. na temat tego, że w pewnych sytuacjach współ-nieobecności są słabszym wskaźnikiem podobieństwa niż współobecności.

i	1,000	0.390	0,176	0,030	00901
	0,390	1,000	0,088	0,140	0,2001
p =	0,176	0,088	1,000	0,600	0,2481
	0,030	0,140	0,600	1000	0,4401
	0,090	0,200	0,248	0,440	1000

Już ogląd macierzy danych ujawnia, że najbardziej podobni są respondenci 3 i 4. Są oni tacy sami ze względu na trzy spośród pięciu cech, co potwierdza współczynnik Gowera = 0,600. Wobec braku negatywnego skojarzenia w od niesieniu do cechy czwartej, a w ślad zatem nadaniu funkcji wskaźnikowej war tości w„ ₄ = i jest to po prostu iloraz liczby zgodnych wartości cech i łącznej liczby cech.

Współczynnik Gowera ma taką konstrukcję, że gd\ wszystkie zmienne są wyłącznie binarne, a współ-nieobecności cech nadano wagę 0. to staje się on współczynnikiem Jaccarda (zob. wzór 4.36

Przypisywanie wag w_n zmiennym nie jest procesem dostatecznie wyrazistym, zwłaszcza gdy zmienne są odmiennych typów, jeżeli w analizie dominują zmienne jednego typy, to można oddzielić zmienne niezgodne i wykorzystać je w uzupełniającej analizie jakościowej (Anderberg (1973) Pomimo utraty części informacji, wskutek zignorowania pewnych zmiennych, analiza będzie prostsza a wpływ uwzględnionych zmiennych łatwiejszy do oceny Jeśli ograniczenie analizy do dominującego typu zmiennych nie będzie zadow alające, to należy rozważyć dwie równoległe, ale odrębne analizy , jedna oparta na zmiennych mierzalnych i druga oparta na zmiennych nominalnych. Porównyw alne podobieństwo obiektów ze względu na obie grupy zmiennych pozw ala wnioskować o analogicznej relacji w przypadku jednego połączonego zbioru zmiennych. Trudniejszy jest zaś przypadek, gdy podobieństwo zachodzi w odniesieniu tylko do jednego zbioru zmiennych. Anderberg stw ierdza, iż nie ma obecnie (tzn. w 1971 r. ) dobrego sposobu łączenia obu analiz. Trudno pow iedzieć, czy Anderberg, pisząc te słowa, znał propozycje Gowera, ale wydaje się, że jego współczynnik podobieństwa jest właśnie pewnym sposobem łączenia różnego typu zmiennych, choć w innym nieco kontekście.

Wybierając miarę podobieństwa, należy odpowiedzieć sobie na pytanie, czy dane powinny być stan dary zowane przed obliczeniem tych miar Większość miar odległości jest czuła na zróżnicow ane skale pomiarowe łub rząd wielkości zmiennych. Ogólnie zmienne o dużym rozproszeniu (np. dużym odchyleniu standardowym) mają większy wpływ na końcową wartość podobieństwa.