8 9

8

Uzwojenie trójfazowe połączone w trójkąt tworzy zamknięty obwód, dla którego w układzie symetrycznym zachodzi zależrSOść:

0    + Uj =0,    (3.10.)

Napięcia międzyprzewodowe równają się napięciom fazowym:

Urs= Ur,	(3.11.)
" Ł? li u	(3.12.)
ii £	(3.13.)
-. • '1 Inaczej: Up = Uf.	(3.14.)
Wierzchołki trójkąta tworzą węzły, w których zbiegają się dwa przewody fazowe i jeden przewód sieciowy. Zgodnie z pierwszym prawem Kirchhoffa geometryczna suma prądów w węźle równa się zeru. Prąd w przewodzie sieciowym równa się różnicy prądów fazowych, ponieważ dla danego węzła jeden z nich jest prądem dopływającym, a drugi odpływającym. Powyższe zależności można zapisać wektorowo:

Ir ~ Irs ~ Itr>	(3.15.)
*—11 Łc II oo'^M 1 sT^1 IXi	(3.16.)
h - Itr ~ Iśt•	(3.17.)
Irs -1 st -Itr -Ify	(3.18.)
Ir -Is ~ h -1p ■	(3.19.)

Zależności między prądami fazowymi i przewodowymi można przedstawić wektorowo (rys. 10).

If

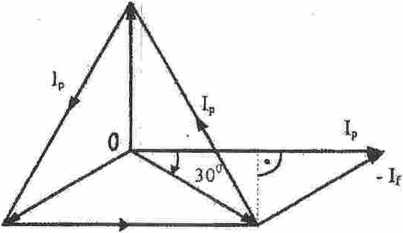
Rys. 10. Wykres wektorowy prądów w układzie trójfazowym symetrycznym połączonym w trójkąt

GT

I_p=2I_f cos 30° =2/_/-y = V37_/    (3.20.)

Prąd przewodowy jest o *J?> większy od prądów fazowych płynących w poszczególnych fazach uzwojenia połączonego w trójkąt.

4. MOC W UKŁADACH TRÓJFAZOWYCH

Moc układu trójfazowego równa się sumie mocy poszczególnych faz. W układach symetrycznych trójfazowych całkowita moc odbiorników równa się sumie mocy odbiorników włączonych w poszczególne fazy.

Gdy odbiornik trójfazowy składa się z trzech jednakowych impedancji fazowych Zf połączonych w guńazdę (rys.l 1.) moc jednej fazy wynosi:

Pf -UfJf COS (p.    (4.1.)

Całkowita moc układu trójfazowego równa się:

P - U. rq1 r cos <pr + U sol S ^cos <Ps ⁺ U tqI T ^cos Vt

Przy założeniu, że Uro ~ U.SO ~ U TO ~ Uf oraz    I_R = I_s = It ~ 1/

(Pr - Vs= (pT= <P

otrzymamy:

P = 3 Pf= 3 UjlfCos(p.

(4.2.)

a)

b)

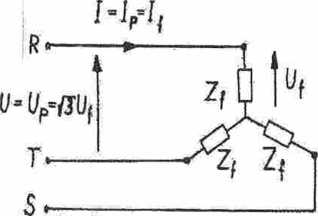
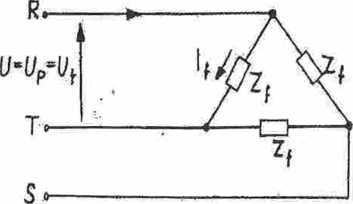
Rys. 11. Schematy układów trójfazowych

a)    połączonego w gwiazdę;

b)    połączonego w trójkąt

Dla układu połączonego w gwiazdę występują zależności: