85167 skrypt0

Ijniowa CvrnowA rn trac.ia opsżumia.iąca sygnałów

-

5.1.1. Podejście geometryczne

Rozważmy (n + I)-wymiarową podprzestrzeń Sjj rozpiętą na obserwacjach (zmiennych losowych) sygnału y

Sq —spon{y(t),y(l- I).....y('-n)}    (5 14)

i załóżmy, że SJj jest podprzestrzenią ośrodkowej przestrzeni Hilberta. rozpiętej przez len sygnał, w której przeliczalny zbiór zmiennych losowych {>•(r t'))"₀, jest zbiorem wszędzie gęstym (zbiór ten rozpina całą przestrzeń i Wówczas ten zbiór można traktować jako bazę wspomnianej przestrzeni Przyjmijmy również, że (nieobserwowany) sygnał losowy <|r) jest statystycznie związany (sko relowany) z obserwowanym sygnałem y (co - w sposób oczywisty wynika np z rys. 5.4). Załóżmy ponadto, że r(r) jest liniowo niezależny od zmiennych losowych {y(/),y(r- I),.. .,y(r - n)}. Gdyby tak nie było, to x(i) - jako element podprzestrzeni SĄ - byłby wyrażony jako kombinacja liniowa tych zmiennych losowych i w konsekwencji otrzymalibyśmy dokładne, tj.. odpowiadające zerowemu błędowi średniokwadratowemu. rozwiązanie problemu liltracii odszu miającej Odrzucając ten trywialny przypadek, odpowiadający sytuacji, kiedy

120

cccciiiie

Liniowa cyfrowa filtracja odszumiająca sygnałów

(^,>(<-*))tt = E<(0y(f-*)=o , k = 0.

5.1.2. Podejście algebraiczne

£

(5.21)

(5.22)

(5.23)

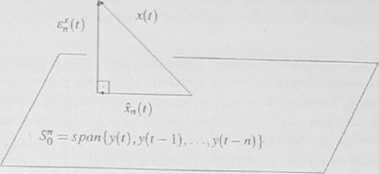
Rys. 5.5. Geometryczne rozwiązanie problemu filtracji odszumiającej

(5.24)

O ■5 O J?	■ CyAn)		' 1
Cxy(0) C(0) .	■ c(-n)		<0	=	0
Cry(/l) c(n) .	■c( 0) .				0

Zmienną losową .{„(t) nazwiemy optymalnym (śrcdniokwndratowo) estymatorem liniowym rzędu n zmiennej losowej x(i). Błąd filtracji, stowarzyszony z estymatorem (5.10), będzie określony jako

<(»)=*(/)-4,(0    (5.11)

a błąd śrcdniokwailratowy

K = ^ «(/))’    (5.12)

będzie zależny wyłącznie od parametrów {a’j}"_₀ filtm

= o.....<n)    (5 13) r;:|

Naszym zadaniem będzie zatem wyznaczenie tych parametrów (czyli odpowiedzi impulsowej filtru odszumiającego), minimalizujących hląd średniokwadra-towy (5.12).

Do tego zagadnienia można podejść zarówno metcxJą algebraiczną (poszukując rozwiązania problemu minimalizacji (5.13) analogicznie jak w punkcie 2.1.1), jak leż geometryczną Tutaj rozważymy podejście geometryczne (w przestrzeni zmiennych losowych), a następnie przedstawimy podejście algebraiczne.

x„[t) jest ortogonalność wektora błędu e*(() względem podprzestrzeni 5J]. Z ko-lei ortogonalność wektora względem podprzestrzeni oznacza ortogonalność cle- K mentu r^(t) względem dowolnego elementu <p(i) € Sjj. Ponieważ bazę pod-przestrzeni SĄ stanowi układ zmiennych losowych {y(f),y(f I).    .,>•(/ n)J, j

zatem dowolny element <p(r) € 5^ wyraża się jako

<5-19) &

Stąd wniosek, że dla spełnienia wymogu ortogonalności błędu £jJ(t) względem podprzestrzeni 5[j wystarczy zażądać, aby element ten był jednocześnie ortogo- ■ nałny względem wszystkich elementów bazy tej podprzestrzeni Proscadzi to do następujących warunków: (5 20)

Z warunków ortogonalności (5.17) wynika natychmiast układ równań liniowych, umożliwiający algebraiczne rozwiązanie problemu liniowej filtracji od-szutniającej. W celu jego wyprowadzenia, zauważmy że

«£(0 = ^X(<) —^n(ł) = -t(r) - X </>'(' - 0 = ^X(‘) + X <■>’(' - 0

/=0 /=0

gdzie

<t=-<i i i = 0,...,n

Z (5.21) i (5.20) wynika, że dla k — 0,____n

-*))« = MO + X<M' - OM' -*))« =

i=0

= M').y(' -*))u+ X<,(y(' -<).)’(' - k))v =

i=0

= E-t(t)y(r -k) + XX,^Ky(^f - OM' ~ ^k) =

1=0

= ^cxy(*) +    - i) -

/=0

= c,y(k) +a^x„₀c(k) + ... + <„r(k - n) =0

Postawienie problemu riLTnAcji OOBZUMIAJACEJ

widmowe gęstości mocy sygnału oryginalnego i szumu leżą w rozdzielnych pasmach częstotliwości, mamy jc(r) <ł SĄ, a w konsekwencji x(t) c 5, gdzie

S = si>an{x{l),S"„)    (5.15)

Rozwiązanie problemu filtracji odszumiającej sprowadza się zatem do wyznaczenia reprezentacji sygnału r(l] 6 S w podprzestrzeni SJ rozpiętej na obserwacjach sygnału zaszumionego, czyli do wyznaczenia elementu f„(t) e SĄ. leżącego w minimalnej (w sensie metryki przestrzeni S) odległości od z(r). Rozwiązanie to wynika - podobnie jak w problemie optymalnej prognozy średnio-kwadralowej, omówionym w punkcie 2.1.2 - z twierdzenia o najlepszej aproksymacji, w myśl którego w podprzestrzeni SĄ istnieje jedyny element

je„(r)4p(sswo e są    (5,i<3)

który leży w najmniejszej odległości od elementu x(r). Oznacza to, że jeśli zdefiniujemy błąd

£„'(') = P(SeSĄ)x(t) = P{(Sl))^L)x(t) = [l-P(SĄ)]x{t) =

= x(r)-f„(r)l SĄ    (5.17)

to

d(x(t),x„(t))u = |1*(») -4«(0llti=    ll«J(0llti= mi"    (⁵ |8)

Sytuację tę ilustmje rys 5.5. Rozwiązanie problemu sprowadza się więc do obliczenia projekcji P(S3)s(r), czyli do wyznaczenia elementu x„(r) Wynika ono. podobnie jak w problemie prognozy średniokwadralowej. z warunków ortogonalności (5.17). Warunkiem ODtymalności rśr«łn;»u..gg| jj

121

msiin

________Postawienie problemu filtracji odszumiającej

gdzie Cxy(i) oznacza kowariancję wzajemną sygnałów x(t) i y(r), zaś c(k) -autokowariancję sygnału y(r)

Zatem z warunków (5 20) otrzymujemy układ (n-l-1) równań liniowych, umożliwiający wyznaczenie parametrów {rr'₀,.. ,crj.n} optymalnego filtru odszumiającego Wyznaczenie tych parametrów umożliwia z kolei obliczenie błędu średniokwadratowego R’„ filtracji odszumiającej. I tak, korzystając z (5.20), mamy

K = e«(0)² =

= (<(/),<('))«=

= «(o.X<M' -«))«=

i-0

= -»))«=

i=0

= «(') .-*('))« =

= W ')+X^<r".M'-o .*('))«=

1=0

= M')M'))u+Ż<»M'-0M'))u =

/=0

= Ex²(r) + X <,Ey(f - i'W0 =

= c_x.(0) + X<,Cvx(i) =

i=0

= c«(0) + a'_n0c_yx (0) +    <„c»x(n)

gdzie c„(0) oznacza wariancję sygnału x(i). zaś c_y,{k) - kowariancję wzajemną sygnałów y(t) i x(r). Wyrażenia (5.24) i (5.23) możemy zapisać łącznie w postaci macierzowej jako

(5.25)

Jest to układ równań normalnych (Youle a-Walkera). stowarzyszony z problemem liniowej filtracji odszumiającej. Zauważmy, że do jego rozwiązania jest wymagana znajomość następujących statystyk sygnałów:

123

122