84176 PC043347

Rozdział 3. Funkcje jednej zmiennej

Twterdzenie 3.3.

Jeśli Ciągi (<*„). (b_n). spełniające warunek a_n < b„ dla n € N, _Są zbiegu wiednio do a, fi, to a < fi.    %

Twierdzenie 3.4. (Twierdzenie o trzech ciągach)

Jeżeli ciągi (a„), (b„), (c„) spełniają warunki:

a)    f\ b„ <a„ U cw,

meN

b)    lim b„ - lim c„ = g,

n—*oo    łi-*oo

to lim On-t

ił-400

Przykład 3.6.

a) Obliczymy granicę ciągu

n

Ponieważ dla każdego n zachodzi nierówność

—1    sin n²    1

g tr <-<

n    n    n

więc rozważany ciąg zbiega do 0 przy    n —* oo.

b) Pokażemy, że granicą ciągu

a„ — ^fn, n e N,

jest liczba 1. Jest to równoważne pokazaniu, że ciąg (a„), gdzie

ifń = a„ + 1    (3J)

jest zbieżny do 0. Podnosząc obie strony równania (3.2) do potęgi n i korzystając ze wzoru Newtona

«pfr    <^a+i>"=Ź (*]“**’"'*•    Mm

otrzymujemy

n(n - 1) ₂    .

n = 1 + na„ +    -a_n + ... + a„.

Ponieważ wszystkie składniki tej sumy są nieujemne, więc nie jest ona mniejsza od każdego swojego składnika. Biorąc trzeci, otrzymujemy

n(n - 1) ₂ n > —2-

czyli dla n > 1 mamy

Z twierdzenia o trzech ciągach wynika, że (a„) jest zbieżny do 0, stąd teza.

3.1. Ciągi liczbowe

Twierdzenie 3.5.

Ciąg zbieżny jest ograniczony. Ponadto ciąg monofoniczny i ograniczony jest zbieżny.

Przykład 3.7.

Pokażemy, te ciąg (a„) o wyrazach 1

a„ =

2^ł+*

jest zbieżny. Zgodnie z twierdzeniem 3.5, wystarczy pokazać, te jest on monofoniczny i ograniczony. Mamy

I “ Of. -

>0,

2"*' + n + 1

czyli ciąg jest rosnący. Ponadto ciąg jest ograniczony, gdyż

^ 1 1

^0<a"^<Z2‘^¹"F^<1-

Wykazaliśmy tym samym, że ciąg jest zbieżny. Nie wskazaliśmy jednak jego granicy -wyznaczenie jej dokładnej wartości jest o wiele bardziej subtelnym problemem.

Twierdzenie 3.6. (Warunek Caućhy’ego zbieżności ciągu)

Ciąg (a„) jest zbieżny wtedy i tylko wtedy, gdy spełniony jest warunek

f\\/ /\ |a_w-Oml<«.

«>0 Ń_ceR n jń>'Ń_s

Przykład 3.8.

Rozważmy jeszcze raz ciąg z przykłada 3.7. Wykażemy, te jest on zbieżny, stosując warunek Cauchy’ego. Niech s > 0 będzie dowolną liczbą. Bez zmniejszenia ogólności możemy założyć, że n > m. Wykorzystując wzór na sumę wyrazów ciągu geometrycznego, mamy

a„ -a,„

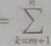
1

2* + *

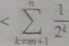
Jeśli więc ^ < e, czyli n > m > log₂ s, to \a„ — a_m\ < s i warunek Cauchy’ego będzie spełniony. Ciąg jest zatem zbieżny.

Definicja 3.5.

Mówimy, że ciąg (a„) dąży do oo, co zapisujemy jako bma« = oo lub a„ —> oo, wtedy i tylko wtedy, gdy

A V Ą    P3>

«>0 N_eeR n>Nf

O takim ciągu mówimy także, iż jest rozbieżny do oo. Mówimy, że ciąg (o*) ma granicę -oo wtedy i tylko wtedy, gdy ciąg (-<*„) dąży do oo.

105