87735 z15 (9)

y

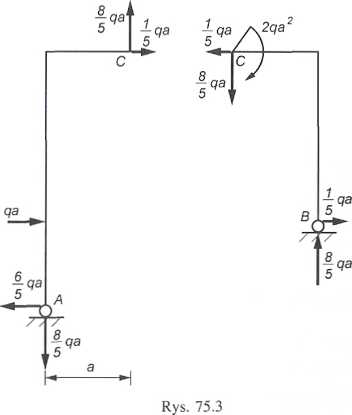
Zauważmy, iż w tym przypadku (rama trójprzegubowa o podporach leżądy(ffl na różnych poziomach) nie da się uniknąć rozwiązywania układu dwóch rów«j nań z dwiema niewiadomymi. Zaprezentowany tu sposób postępowania (wyhóp odpowiednich równań równowagi odpowiednich części układu) nie jest jedynymi możliwym. Równie dobrze można na przykład pisać warunki:

uMiid ACB M_a - O,

itmt cb y, ^Mc= °»

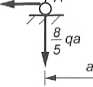
|t)il Już można obliczyć reakcje V_B, H_B itd. 'MIANIE 76

lit)/, wiązać ramę pokazaną na rys. 76.1.

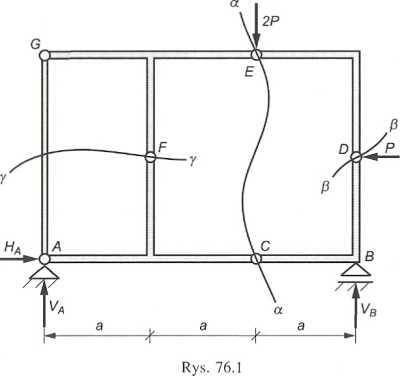
Mozwlązanie

Kama ta ma bardziej złożoną budowę niż ramy liczone wcześniej. Tu do Obliczenia mamy reakcje więzów zewnętrznych (punkty A i B) i wewnętrznych |||, oddziaływania w przegubach C, D, E, F i siłę w ściągu GA) — łącznie jest W|C dwanaście niewiadomych. Istotne jest przyjęcie odpowiedniej kolejności postępowania, tak aby uniknąć układu równań z niewiadomymi. Zawsze po-|n iiwne jest ciącie ramy przez przeguby i pręty dwuprzegubowe — problem tkwi liczbie wprowadzanych przez tę operację na danym etapie niewiadomych.

[ Zauważmy, że część prawa układu CBDE to rama trój przegubowa, zaś lewa fACIE — to rama ze ściągiem. Tak więc, stosując zasadę uwalniania od wię-|rtw, a mówiąc krótko, tnąc ramę przekrojem ct-a a następnie (3-p i y-y, mamy sytuację pokazaną na rys. 76.2 i 76.3.

Jest oczywiste, że spełnione tu być muszą równania równowagi globalnej (ryi. 76.1) oraz lokalnej — poszczególnych prętów ramy (rys. 76.2, 76.3).

Chcąc iść po sznurku, tj. zuwnzc otrzymywać równanie zawierające jedną nową niewiadomą, nuleży poNtąpić następująco:

193