226 (17)

J

h-^r=V₂ ~~j

Rys. 143. Określenie momentów gnących

W punkcie A wielkość Mg₀ = 0, gdyż suma momentów gnących w tym miejscu jest równa 0. W kolejnych punktach przekroju otrzymamy następujące wartości:

Mg_r = 1 • R_a - 1 • q ■ 0,5 = 1 • 3,75 - 1 • 1 • 0,5 = 3,25 N • m Mg₂ = 2 ■ R_A — 2 ■ q ■ l — 2 ■ 3,75 -211 = 5,5 N • m

Mg₃ = 3 • R_a — 3 • ą • 1,5 = 11,25 - 3 • 1 • 1,5 = 6,75 N • m

Mg₈ = & ■ R_A — & • q ■ 4 = 8 • 3,75 — 814= -2- N - m

Mg₉ = 9 ■ R_a - 9 ■ q ■ 4,5 + 1 • R_g = 9 ■ 3,75 - 9 • 1 • 4,5 + 6,25 • 1 =

= -0,5 N-m

Mg₁₀ = 10 • R_a - 10 • q ■ 5 + 2 ■ R_B = 10 ■ 3,75 - 10 ■ 1 • 5 + 6,25 -2 = 0

Wykres momentów gnących występujących w belce przedstawia rys. 141c.

Istnieje również inny, w niektórych wypadkach wygodniejszy, sposób obliczania momentów gnących. Otóż można udowodnić, że krzywa momentów gnących jest krzywą całkową krzywej sił tnących. Oznacza to, że rzędne wykresu momentów gnących można określić obliczając odpowiednie powierzchnie pod krzywą sił tnących. Jeżeli do pierwszego odcinka badanej belki (w zakresie 0 — 0,8 /) zastosujemy tę metodę obliczeń i określimy pole trapezu utworzonego przez ten wykres to otrzymamy wzór ogólny:

^M9i = l (2R_A-q-l_t)

a po przekształceniu:

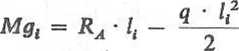
czyli postać identyczną jak równanie 14.9.

madę by voyteck (dec‘2004)

226