234 (49)

METODY NUMERYCZNE...

Zadanie przybliżone dla (10.101) przyjmuje więc postać: wyznaczyć taką funkcję u,, e Vjf\ że

(10.102)

a (i/*, p) = i (t>) _t i> g V?-

Można pokazać, że forma a (u, p) jest //^-eliptyczna i ciągła oraz że /(i») jest funkcjonałem ograniczonym. Implikuje to istnienie jednoznacznego rozwiązania zadania (10.102) i jego stabilność. Szybkość zbieżności tego wariantu M ES wynika z następującego twierdzenia, które podajemy bez dowodu (zob. np. poz. [141):

Twierdzenie 10.24

Jeśli rozwiązanie ir zagadnienia (10.100) jest takie, że ue // ‘(0,/) n //*(0./), to gdzie u_h jest rozwiązaniem zadania (10,102), zaś M jest stałą dodatnią niezależną od h.

Określimy układ równań algebraicznych, odpowiadający zadaniu (10.102). Funkcje bazowe t/^;;' i i/‘^; przestrzeni K'³' wyznaczyliśmy wyżej. Rozwiązania przybliżonego u_h szukamy w postaci

m

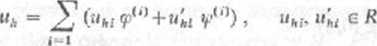
Zauważmy, żc u_fil i u'_hl są wartościami funkcji u_h i jej pochodnej w punkcie

Jlfj = //*.

Przy oznaczeniach

K =    .... f(n<(n^r

układ równań ma postać ■\ = /»

Macierz A_a wymiaru 2«j x 2in jest macierzą 7-diagonulną, co łatwo jest sprawdzić. Można pokazać, z.c A_h jest macierzą symetryczną i dodatnio określoną.

W zadaniach rozpatrywanych wyżej zakładaliśmy jednorodność warunków zasadniczych (Dirichleta). Jeśli warunki te nie są jednorodne, to postępujemy w następujący sposób. Rozwiązania u zagadnienia wyjściowego poszukujemy w postaci u = w + r, gd/ie v jest daną funkcją spełniającą warunki brzegowe. Taką funkcję v jest łatwo znaleźć w przypadku zagadnień dla równań zwyczajnych. Podstawiając u = w+v do zagadnienia wyjściowego otrzymujemy zagadnienie dla funkcji k* już z jednorodnymi warunkami brzegowymi.

Przy konstrukcji MES dla zadań z warunkami niejednorodnymi (zasadniczymi) możemy też postąpić inaczej. Rozwiązania przybliżonego będziemy poszukiwać w przestrzeni elementu skończonego, której funkcje nie spełniają warunków zasadniczych. Warunki te ma spełniać tylko rozwiązanie przybliżone. Otrzymane stąd równania dołączamy do zadania przybliżonego.