235 (47)

235

235

9.2. Przykłady obliczania prędkości bezwzględnych i przyepieereh ROZWIĄZANI!

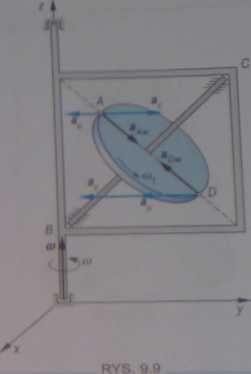
Przyspieszenie względne punktu A ma zwrot jak na ry*. 0.9 L I    i jego wartość jest równa

= co²b-^~

Ptzyspieszenie unoszenia w tym przypadku jest skierowane do osi obrotu ramki i jego wartość wynosi

Ponieważ prędkość względna punktu A ma zwrot osi v. więc przyspieszenie Coriolisa a_c = 2o> x v_w ma zwrot /godny z osią >• i jego wartość jest równa

a_c = 2oxo\ R — bto²

Rzuty bezwzględnego przyspieszenia na osie układu współrzędnych wynoszą

a_bx =0

•Jl 5    ₂

a_by = a_c - a_u + a_w— = -ba>^Ł

\/2 ba)²

^abz = ~^a*~Y ⁼ ~

Wartość przyspieszenia bezwzględnego jest równa

V29, ₂

a_b = —ba)*

4

Składowe przyspieszenia bezwzględnego punktu D mają zwroty jak na rys. 9.9, a ich wartości są równe

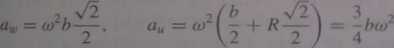
a_c = co²b

Wartość przyspieszenia bezwzględnego punktu D wynosi

bco² r— a_b = —— • \/85 4

Płaszczyzna Ox\y\ obraca się ze stałą prędkością kątową co PRZYKŁAD 9.9 wokół osi z, w kierunku zgodnym z ruchem wskazówek zegara. Po płaszczyźnie porusza się punkt A zgodnie z równu-niem x\ = r(l +coso>r), vi = r sin tur. Znaleźć bezwzględne przyspieszenie punktu A.