26 27 (4)

I'^¹¹

ftanjtjgj 1.7

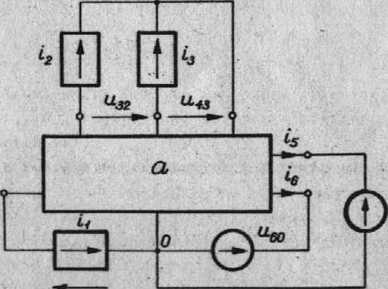
V obwodzie rezystancyjnym (rys. 1.16) nożna wyodrębnić 3 bloki ele-•ntów pasywnych: dwójnik JD_B (bieguny 0, 1), trójnik    (bieguny

, 3» 4) i trójnik T_c (bieguny O, 5, 6). Dane są ioh parametry w poetatr    _

- rezystancja dwójnika _a>

10

- macierz współczynników (w Jednostkach j)

L^r3 ^Tk

iążąoa wektor napięć

[^Go]

ca

trójnika J", z woktorem prądów

KT-

«, e₂l

^e3 J

macierz współczynników (w jednostkach y)

ia

trójnika 7”₀ z wektorem napięć

[3-

iąząoa wektor prądów

Orientacje napięć i prądów, dla których obowiązują zależności:

*10

% zaznaczone na rysunku.

Ułożyć zrównanie maoierzowe opisujące wektor wielkości wyj 4 o i o-y o h

‘1

*2

*3

“50

^u60

~ i.

7] =

raktując parametry R, e, J jako dane.

Postawiony problem sugeruje możliwość dokonania analizy 7-hiegunowogo bwodn aktywnego (bieguny 0, 1, 2,.... 6) w oderwaniu nie tylko od struk-ury bloków pasywnych (której nie znamy), ale również od ich charakterys-yki napięciowo-prądoweJ. Hipoteza tego rodzaju wymaga jednak motywacji, dyż zdaje się zaprzeczać przekonaniu o zależności dowolnej składowej dpowiedzi obwodu od wszystkich (na ogól) parametrów aktywnych i pasyw-iych.

Aby oddalić tę wątpliwość, cauwatojr przede wszystkim, że składowe aktora y] tworzą zbiór ni ezależnyoh prądów i napięć,

27

to znaczy, że na te wielkości nie są nałożone więzy wynikające z postulatów Kirohhoffa.

Dzięki temu, w myśl twierdzenia o kompensacji, można zastąpić bloki pasywne źródłami prądu i napięcia (rys. 1.17)» które reprezentują składowe wektora y] i nie wprowadzają żadnych zmian prądów 1 napięć "wewnątrz" 7-biogunnika aktywnego CL, Jak również "zewnętrznych" napięć

^U10’ ^u23’ ^u3fc ^orass P^r*^d6w *₅» ⁱó*

^uso

Rys. 1.17